Having no solves yet in the rev category with one day remaining in corCTF 2024, I decided to have a gander at something that looked approachable. The two easiest challenges at the time by solve count were corMine: The Beginning and its sequel corMine 2: Revelations, which was a game of some sort. However, I eventually gave up after 5+ minutes trying to get the game to just run! But I guess I don’t feel so bad seeing as my teammates couldn’t figure it out either :’)
The next easiest one on the list was called digest-me, which is the topic of this post and what I poured most of my time on for the next 24 hours. Luckily, this one was a simple binary that asked you to input a flag, and told you whether it was correct. These kinds of programs are common enough in CTFs that they adopt a not-so-special name called a flag checker.
Challenge
The description gives us a few clues, perhaps it has something to do with hashing and bits (?), but otherwise just contains the average lore.
FizzBuzz101 was innocently writing a new, top-secret compiler when his computer was Crowdstriked. Worse, the recovery key is behind a hasher that he wrote and compiled himself, and he can’t remember how the bits work! Can you help him get his life’s work back?
Here is a sample interaction from the digestme binary:
$ ./digestme
Welcome!
Please enter the flag here:
corctf{what}
Try again:
corctf{potatoes}
Try again:
It’s too big
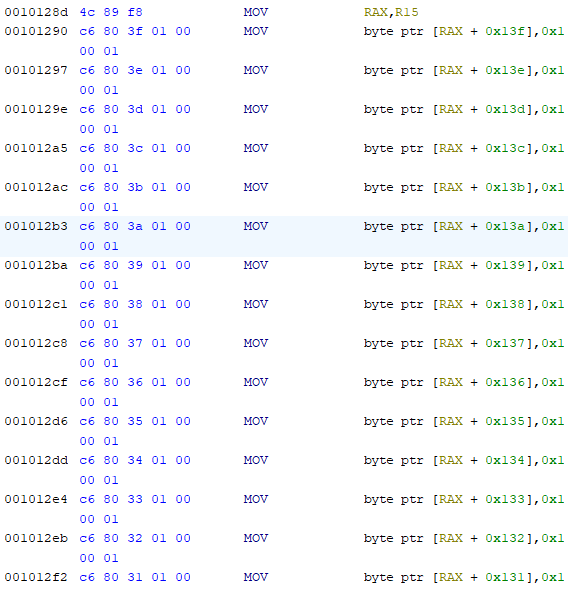
One problem immediately came up when opening the program in Ghidra – it refused to decompile
main()! Examining the disassembly to see what could possibly have went wrong, I was horrified to
witness a chain of about 300,000 instructions consisting solely of mov, and, or and xor:
Luckily, I worked around this by patching ret instructions near the top and bottom of main() to
ensure Ghidra doesn’t try to decompile all of it. That allows us to finally see the start of the
function.
Brute force?
Through a combination of static and dynamic analysis, I was able to constrain the flag to a set of
preconditions that were enforced by those ifs:
len(flag) == 19
flag[:7] == "corctf{"
flag[8] == flag[17]
flag[9] == flag[11]
flag[7] == flag[16] + 1
flag[14] == flag[16] + 4
The short flag certainly raised my eyebrows about the possibility of brute force. There were 11
unknown bytes but 4 of those can be disregarded because of the extra constraints, for a total of
95^7 = 69,833,729,609,375 possible flags (assuming the flag is printable).
However, it’s worth noting that each run would require at least 300,000 instructions, and 2 days
would not nearly be enough to find the flag in time on my poor 4-core Intel-i5 laptop.
The rest of the program is focused on executing the said 300,000 instructions, which judging by the
disassembly just seems to be a bunch of operations on an array. A is initialized at the start via
A = (byte *)calloc(1,100000), which allocates a zero-filled 100,000-byte array.
The flag is then loaded into A by converting each byte inside corctf{...} into 8 bits, and then
loading the bits starting from the offset *(A+0x940) in big-endian order. For those who speak
Python, that looks something like this:
A[0x940:0x998] = [(c >> i) & 1 for c in code[7:-1] for i in range(7, -1, -1)]
After the extremely long chain of array operations, the first 128 bits of A are converted into
4 32-bit integers (call them a, b, c, d). The flag checker outputs Nice! if
c == 0x19c603b and d == 0x14353ce (A.K.A. the target condition).
Reversing the elephant in the room
Now that it was clear how the program was checking the flag, I worked on parsing the long array operations into something more readable. Once we had the instructions in a higher-level language, it would be possible in theory to rely on z3 to recover the flag for us.
Instead of bashing Ghidra to decompile everything for us, I used capstone to parse the machine
code into a clean disassembly:
from capstone import *
with open('digestme', 'rb') as f:
binary = f.read()
code = binary[0x1290:0xed854]
cs = Cs(CS_ARCH_X86, CS_MODE_64)
instructions = cs.disasm(code, 0)
for inst in instructions:
print(inst.mnemonic, inst.op_str)
After combing through the output, I was surprised to find only two distinct groups of instructions.
It was either a simple mov in the form,
mov byte ptr [rax + X], Y
which maps to A[X] = Y, or
mov cl, byte ptr [rax + X]
<op> cl, byte ptr [rax + Y]
mov byte ptr [rax + Z], cl
which maps to A[Z] = A[X] <op> A[Y] where <op> ∈ [and, or, xor].
This made it relatively easy to decompile with a little bit of regex:
from capstone import *
import re
with open('digestme', 'rb') as f:
binary = f.read()
OP_MAP = {'and': '&', 'or': '|', 'xor': '^'}
code = binary[0x1290:0xed854]
cs = Cs(CS_ARCH_X86, CS_MODE_64)
instructions = cs.disasm(code, 0)
commands = []
while (inst := next(instructions, None)) is not None:
assert inst.mnemonic == 'mov'
if m := re.fullmatch(r'byte ptr \[rax( \+ (\w+)|)\], ([01])', inst.op_str):
out = int(m[2], 0) if m[2] else 0
val = int(m[3])
commands.append(f'A[{out:#x}] = {val}')
else:
m = re.fullmatch(r'cl, byte ptr \[rax( \+ (\w+)|)\]', inst.op_str)
in1 = int(m[2], 0) if m[2] else 0
inst = next(instructions)
m = re.fullmatch(r'cl, byte ptr \[rax( \+ (\w+)|)\]', inst.op_str)
in2 = int(m[2], 0) if m[2] else 0
op = OP_MAP[inst.mnemonic]
inst = next(instructions)
m = re.fullmatch(r'byte ptr \[rax( \+ (\w+)|)\], cl', inst.op_str)
out = int(m[2], 0) if m[2] else 0
commands.append(f'A[{out:#x}] = A[{in1:#x}] {op} A[{in2:#x}]')
print(len(commands))
with open('commands.txt', 'w') as f:
for cmd in commands:
f.write(cmd + '\n')
I also printed out the number of commands, which came out at a respectable 60,180. Still far from being ideal of course.
Given the description of the challenge, I figured this was some hashing algorithm that was
obfuscated by bit manipulations. Looking through the commands.txt file, I noticed that there was a
lot of repetition. In fact, it almost always performed one of &, |, or ^ in 32-bit chunks like
this:
A[0x0] = A[0xfa0] | A[0x100]
A[0x1] = A[0xfa1] | A[0x101]
A[0x2] = A[0xfa2] | A[0x102]
A[0x3] = A[0xfa3] | A[0x103]
...
A[0x1f] = A[0xfbf] | A[0x11f]
However, there were also certain chunks that had all the operators combined in a mixed order, which
strangely always came in groups of 157 that repeated ^, ^, &, &, | cylically.
A[0xe7] = A[0xc7] ^ A[0x27]
A[0xb40] = A[0xc7] & A[0x27]
A[0xb41] = A[0xc6] ^ A[0x26]
A[0xe6] = A[0xb41] ^ A[0xb40]
A[0xb40] = A[0xb41] & A[0xb40]
A[0xb41] = A[0xc6] & A[0x26]
A[0xb40] = A[0xb41] | A[0xb40]
A[0xb41] = A[0xc5] ^ A[0x25]
A[0xe5] = A[0xb41] ^ A[0xb40]
A[0xb40] = A[0xb41] & A[0xb40]
A[0xb41] = A[0xc5] & A[0x25]
A[0xb40] = A[0xb41] | A[0xb40]
A[0xb41] = A[0xc4] ^ A[0x24]
A[0xe4] = A[0xb41] ^ A[0xb40]
A[0xb40] = A[0xb41] & A[0xb40]
At first, this made me scratch my head as it did not seem to “fit” with the rest of the output. But then I realized that this obscure-looking block of code was actually implementing a 32-bit adder!
This finally made sense with the rest of the logic, and once I was certain that these were all indeed 32-bit operations implemented on bits, I quickly hacked together a second program to convert the 60,180 commands into a new set of commands performed on 32-bit integers:
import re
def MOV(cmd):
m = re.fullmatch(r'A\[(\w+)\] = ([01])', cmd)
if m is None:
return None
return int(m[1], 0), int(m[2])
def BITW(cmd):
m = re.fullmatch(r'A\[(\w+)\] = A\[(\w+)\] ([\^|&]) A\[(\w+)\]', cmd)
if m is None:
return None
return int(m[1], 0), m[3], int(m[2], 0), int(m[4], 0)
with open('commands.txt', 'r') as f:
commands = list(map(str.rstrip, f))
ncommands = []
idx = 0
while idx < len(commands):
cmd = commands[idx]
if MOV(cmd):
chunk = commands[idx:idx+32]
outs, vals = zip(*[MOV(cmd) for cmd in chunk])
assert outs == tuple(range(outs[0], outs[-1] - 1, -1)) and outs[-1] & 31 == 0
val = 0
for o, v in zip(outs, vals):
i = o & 31
val |= v << 8 * (i // 8) + 7 - (i % 8)
ncommands.append(f'A[{outs[-1]>>5}] = {val:#x}')
idx += 32
elif BITW(cmd) and BITW(cmd)[1] == BITW(commands[idx + 1])[1]:
chunk = commands[idx:idx+32]
outs, ops, in1s, in2s = zip(*[BITW(cmd) for cmd in chunk])
if outs[0] & 31 == 0:
assert outs == tuple(range(outs[0], outs[-1] + 1)) and outs[0] & 31 == 0
assert len(set(ops)) == 1
assert in1s == tuple(range(in1s[0], in1s[-1] + 1)) and in1s[0] & 31 == 0
assert in2s == tuple(range(in2s[0], in2s[-1] + 1)) and in2s[0] & 31 == 0
ncommands.append(f'A[{outs[0]>>5}] = A[{in1s[0]>>5}] {ops[0]} A[{in2s[0]>>5}]')
else:
rotl = (outs.index(min(outs) + 7) + 1) & 31
ncommands.append(f'A[{outs[0]>>5}] = rotl(A[{in1s[0]>>5}] {ops[0]} A[{in2s[0]>>5}], {rotl})')
assert [in1s[24 - 8 * (i // 8) + (i % 8)] - min(in1s) == i for i in range(32)]
assert [in2s[24 - 8 * (i // 8) + (i % 8)] - min(in2s) == i for i in range(32)]
idx += 32
else:
chunk = commands[idx:idx+157]
outs, ops, in1s, in2s = zip(*[BITW(cmd) for cmd in chunk])
assert outs.count(0xb40) == 63 and outs.count(0xb41) == 62
assert ops == ('^', '&') + ('^', '^', '&', '&', '|') * 31
assert in1s.count(0xb40) == 0 and in1s.count(0xb41) == 93
assert in2s.count(0xb40) == 93 and in2s.count(0xb41) == 0
assert outs[33] & 31 == 0 and in1s[32] & 31 == 0 and in2s[32] & 31 == 0
ncommands.append(f'A[{outs[33]>>5}] = A[{in1s[32]>>5}] + A[{in2s[32]>>5}]')
idx += 157
print(len(ncommands))
with open('commands2.txt', 'w') as f:
for cmd in ncommands:
f.write(cmd + '\n')
There were some tricky implementation details like rotl() somehow being part of the logic, but in
the end we are left with a much simpler program with “only” 865 lines:
A[9] = 0xffffffff
A[125] = 0x0
A[126] = 0x0
A[127] = 0x0
A[128] = 0x0
A[0] = A[125] | A[8]
A[1] = A[126] | A[8]
A[2] = A[127] | A[8]
A[3] = A[128] | A[8]
A[10] = 0xd76aa478
A[11] = 0xe8c7b756
A[12] = 0x242070db
A[13] = 0xc1bdceee
A[14] = 0xf57c0faf
A[15] = 0x4787c62a
A[16] = 0xa8304613
A[17] = 0xfd469501
A[18] = 0x698098d8
A[19] = 0x8b44f7af
A[20] = 0xffff5bb1
A[21] = 0x895cd7be
A[22] = 0x6b901122
A[23] = 0xfd987193
A[24] = 0xa679438e
A[25] = 0x49b40821
A[26] = 0xf61e2562
A[27] = 0xc040b340
A[28] = 0x265e5a51
A[29] = 0xe9b6c7aa
A[30] = 0xd62f105d
A[31] = 0x2441453
A[32] = 0xd8a1e681
A[33] = 0xe7d3fbc8
A[34] = 0x21e1cde6
A[35] = 0xc33707d6
A[36] = 0xf4d50d87
A[37] = 0x455a14ed
A[38] = 0xa9e3e905
A[39] = 0xfcefa3f8
A[40] = 0x676f02d9
A[41] = 0x8d2a4c8a
A[42] = 0xfffa3942
A[43] = 0x8771f681
A[44] = 0x6d9d6122
A[45] = 0xfde5380c
A[46] = 0xa4beea44
A[47] = 0x4bdecfa9
A[48] = 0xf6bb4b60
A[49] = 0xbebfbc70
A[50] = 0x289b7ec6
A[51] = 0xeaa127fa
A[52] = 0xd4ef3085
A[53] = 0x4881d05
A[54] = 0xd9d4d039
A[55] = 0xe6db99e5
A[56] = 0x1fa27cf8
A[57] = 0xc4ac5665
A[58] = 0xf4292244
A[59] = 0x432aff97
A[60] = 0xab9423a7
A[61] = 0xfc93a039
A[62] = 0x655b59c3
A[63] = 0x8f0ccc92
A[64] = 0xffeff47d
A[65] = 0x85845dd1
A[66] = 0x6fa87e4f
A[67] = 0xfe2ce6e0
A[68] = 0xa3014314
A[69] = 0x4e0811a1
A[70] = 0xf7537e82
A[71] = 0xbd3af235
A[72] = 0x2ad7d2bb
A[73] = 0xeb86d391
A[5] = A[1] & A[2]
A[6] = A[1] ^ A[9]
A[7] = A[6] & A[3]
A[4] = A[5] | A[7]
A[5] = A[4] + A[0]
A[6] = A[5] + A[74]
A[4] = A[6] + A[10]
A[0] = A[3] | A[8]
A[3] = A[2] | A[8]
A[2] = A[1] | A[8]
A[6] = rotl(A[4] | A[8], 7)
A[7] = A[6] + A[1]
A[1] = A[7] | A[8]
A[5] = A[1] & A[2]
A[6] = A[1] ^ A[9]
A[7] = A[6] & A[3]
A[4] = A[5] | A[7]
A[5] = A[4] + A[0]
A[6] = A[5] + A[75]
A[4] = A[6] + A[11]
A[0] = A[3] | A[8]
A[3] = A[2] | A[8]
A[2] = A[1] | A[8]
A[6] = rotl(A[4] | A[8], 12)
A[7] = A[6] + A[1]
A[1] = A[7] | A[8]
A[5] = A[1] & A[2]
A[6] = A[1] ^ A[9]
A[7] = A[6] & A[3]
A[4] = A[5] | A[7]
A[5] = A[4] + A[0]
A[6] = A[5] + A[76]
A[4] = A[6] + A[12]
A[0] = A[3] | A[8]
A[3] = A[2] | A[8]
A[2] = A[1] | A[8]
A[6] = rotl(A[4] | A[8], 17)
A[7] = A[6] + A[1]
A[1] = A[7] | A[8]
A[5] = A[1] & A[2]
A[6] = A[1] ^ A[9]
A[7] = A[6] & A[3]
A[4] = A[5] | A[7]
A[5] = A[4] + A[0]
A[6] = A[5] + A[77]
A[4] = A[6] + A[13]
A[0] = A[3] | A[8]
A[3] = A[2] | A[8]
A[2] = A[1] | A[8]
A[6] = rotl(A[4] | A[8], 22)
A[7] = A[6] + A[1]
A[1] = A[7] | A[8]
A[5] = A[1] & A[2]
A[6] = A[1] ^ A[9]
A[7] = A[6] & A[3]
A[4] = A[5] | A[7]
A[5] = A[4] + A[0]
A[6] = A[5] + A[78]
A[4] = A[6] + A[14]
A[0] = A[3] | A[8]
A[3] = A[2] | A[8]
A[2] = A[1] | A[8]
A[6] = rotl(A[4] | A[8], 7)
A[7] = A[6] + A[1]
A[1] = A[7] | A[8]
A[5] = A[1] & A[2]
A[6] = A[1] ^ A[9]
A[7] = A[6] & A[3]
A[4] = A[5] | A[7]
A[5] = A[4] + A[0]
A[6] = A[5] + A[79]
A[4] = A[6] + A[15]
A[0] = A[3] | A[8]
A[3] = A[2] | A[8]
A[2] = A[1] | A[8]
A[6] = rotl(A[4] | A[8], 12)
A[7] = A[6] + A[1]
A[1] = A[7] | A[8]
A[5] = A[1] & A[2]
A[6] = A[1] ^ A[9]
A[7] = A[6] & A[3]
A[4] = A[5] | A[7]
A[5] = A[4] + A[0]
A[6] = A[5] + A[80]
A[4] = A[6] + A[16]
A[0] = A[3] | A[8]
A[3] = A[2] | A[8]
A[2] = A[1] | A[8]
A[6] = rotl(A[4] | A[8], 17)
A[7] = A[6] + A[1]
A[1] = A[7] | A[8]
A[5] = A[1] & A[2]
A[6] = A[1] ^ A[9]
A[7] = A[6] & A[3]
A[4] = A[5] | A[7]
A[5] = A[4] + A[0]
A[6] = A[5] + A[81]
A[4] = A[6] + A[17]
A[0] = A[3] | A[8]
A[3] = A[2] | A[8]
A[2] = A[1] | A[8]
A[6] = rotl(A[4] | A[8], 22)
A[7] = A[6] + A[1]
A[1] = A[7] | A[8]
A[5] = A[1] & A[2]
A[6] = A[1] ^ A[9]
A[7] = A[6] & A[3]
A[4] = A[5] | A[7]
A[5] = A[4] + A[0]
A[6] = A[5] + A[82]
A[4] = A[6] + A[18]
A[0] = A[3] | A[8]
A[3] = A[2] | A[8]
A[2] = A[1] | A[8]
A[6] = rotl(A[4] | A[8], 7)
A[7] = A[6] + A[1]
A[1] = A[7] | A[8]
A[5] = A[1] & A[2]
A[6] = A[1] ^ A[9]
A[7] = A[6] & A[3]
A[4] = A[5] | A[7]
A[5] = A[4] + A[0]
A[6] = A[5] + A[83]
A[4] = A[6] + A[19]
A[0] = A[3] | A[8]
A[3] = A[2] | A[8]
A[2] = A[1] | A[8]
A[6] = rotl(A[4] | A[8], 12)
A[7] = A[6] + A[1]
A[1] = A[7] | A[8]
A[5] = A[1] & A[2]
A[6] = A[1] ^ A[9]
A[7] = A[6] & A[3]
A[4] = A[5] | A[7]
A[5] = A[4] + A[0]
A[6] = A[5] + A[84]
A[4] = A[6] + A[20]
A[0] = A[3] | A[8]
A[3] = A[2] | A[8]
A[2] = A[1] | A[8]
A[6] = rotl(A[4] | A[8], 17)
A[7] = A[6] + A[1]
A[1] = A[7] | A[8]
A[5] = A[1] & A[2]
A[6] = A[1] ^ A[9]
A[7] = A[6] & A[3]
A[4] = A[5] | A[7]
A[5] = A[4] + A[0]
A[6] = A[5] + A[85]
A[4] = A[6] + A[21]
A[0] = A[3] | A[8]
A[3] = A[2] | A[8]
A[2] = A[1] | A[8]
A[6] = rotl(A[4] | A[8], 22)
A[7] = A[6] + A[1]
A[1] = A[7] | A[8]
A[5] = A[1] & A[2]
A[6] = A[1] ^ A[9]
A[7] = A[6] & A[3]
A[4] = A[5] | A[7]
A[5] = A[4] + A[0]
A[6] = A[5] + A[86]
A[4] = A[6] + A[22]
A[0] = A[3] | A[8]
A[3] = A[2] | A[8]
A[2] = A[1] | A[8]
A[6] = rotl(A[4] | A[8], 7)
A[7] = A[6] + A[1]
A[1] = A[7] | A[8]
A[5] = A[1] & A[2]
A[6] = A[1] ^ A[9]
A[7] = A[6] & A[3]
A[4] = A[5] | A[7]
A[5] = A[4] + A[0]
A[6] = A[5] + A[87]
A[4] = A[6] + A[23]
A[0] = A[3] | A[8]
A[3] = A[2] | A[8]
A[2] = A[1] | A[8]
A[6] = rotl(A[4] | A[8], 12)
A[7] = A[6] + A[1]
A[1] = A[7] | A[8]
A[5] = A[1] & A[2]
A[6] = A[1] ^ A[9]
A[7] = A[6] & A[3]
A[4] = A[5] | A[7]
A[5] = A[4] + A[0]
A[6] = A[5] + A[88]
A[4] = A[6] + A[24]
A[0] = A[3] | A[8]
A[3] = A[2] | A[8]
A[2] = A[1] | A[8]
A[6] = rotl(A[4] | A[8], 17)
A[7] = A[6] + A[1]
A[1] = A[7] | A[8]
A[5] = A[1] & A[2]
A[6] = A[1] ^ A[9]
A[7] = A[6] & A[3]
A[4] = A[5] | A[7]
A[5] = A[4] + A[0]
A[6] = A[5] + A[89]
A[4] = A[6] + A[25]
A[0] = A[3] | A[8]
A[3] = A[2] | A[8]
A[2] = A[1] | A[8]
A[6] = rotl(A[4] | A[8], 22)
A[7] = A[6] + A[1]
A[1] = A[7] | A[8]
A[5] = A[3] & A[1]
A[6] = A[3] ^ A[9]
A[7] = A[6] & A[2]
A[4] = A[5] | A[7]
A[5] = A[4] + A[0]
A[6] = A[5] + A[75]
A[4] = A[6] + A[26]
A[0] = A[3] | A[8]
A[3] = A[2] | A[8]
A[2] = A[1] | A[8]
A[6] = rotl(A[4] | A[8], 5)
A[7] = A[6] + A[1]
A[1] = A[7] | A[8]
A[5] = A[3] & A[1]
A[6] = A[3] ^ A[9]
A[7] = A[6] & A[2]
A[4] = A[5] | A[7]
A[5] = A[4] + A[0]
A[6] = A[5] + A[80]
A[4] = A[6] + A[27]
A[0] = A[3] | A[8]
A[3] = A[2] | A[8]
A[2] = A[1] | A[8]
A[6] = rotl(A[4] | A[8], 9)
A[7] = A[6] + A[1]
A[1] = A[7] | A[8]
A[5] = A[3] & A[1]
A[6] = A[3] ^ A[9]
A[7] = A[6] & A[2]
A[4] = A[5] | A[7]
A[5] = A[4] + A[0]
A[6] = A[5] + A[85]
A[4] = A[6] + A[28]
A[0] = A[3] | A[8]
A[3] = A[2] | A[8]
A[2] = A[1] | A[8]
A[6] = rotl(A[4] | A[8], 14)
A[7] = A[6] + A[1]
A[1] = A[7] | A[8]
A[5] = A[3] & A[1]
A[6] = A[3] ^ A[9]
A[7] = A[6] & A[2]
A[4] = A[5] | A[7]
A[5] = A[4] + A[0]
A[6] = A[5] + A[74]
A[4] = A[6] + A[29]
A[0] = A[3] | A[8]
A[3] = A[2] | A[8]
A[2] = A[1] | A[8]
A[6] = rotl(A[4] | A[8], 20)
A[7] = A[6] + A[1]
A[1] = A[7] | A[8]
A[5] = A[3] & A[1]
A[6] = A[3] ^ A[9]
A[7] = A[6] & A[2]
A[4] = A[5] | A[7]
A[5] = A[4] + A[0]
A[6] = A[5] + A[79]
A[4] = A[6] + A[30]
A[0] = A[3] | A[8]
A[3] = A[2] | A[8]
A[2] = A[1] | A[8]
A[6] = rotl(A[4] | A[8], 5)
A[7] = A[6] + A[1]
A[1] = A[7] | A[8]
A[5] = A[3] & A[1]
A[6] = A[3] ^ A[9]
A[7] = A[6] & A[2]
A[4] = A[5] | A[7]
A[5] = A[4] + A[0]
A[6] = A[5] + A[84]
A[4] = A[6] + A[31]
A[0] = A[3] | A[8]
A[3] = A[2] | A[8]
A[2] = A[1] | A[8]
A[6] = rotl(A[4] | A[8], 9)
A[7] = A[6] + A[1]
A[1] = A[7] | A[8]
A[5] = A[3] & A[1]
A[6] = A[3] ^ A[9]
A[7] = A[6] & A[2]
A[4] = A[5] | A[7]
A[5] = A[4] + A[0]
A[6] = A[5] + A[89]
A[4] = A[6] + A[32]
A[0] = A[3] | A[8]
A[3] = A[2] | A[8]
A[2] = A[1] | A[8]
A[6] = rotl(A[4] | A[8], 14)
A[7] = A[6] + A[1]
A[1] = A[7] | A[8]
A[5] = A[3] & A[1]
A[6] = A[3] ^ A[9]
A[7] = A[6] & A[2]
A[4] = A[5] | A[7]
A[5] = A[4] + A[0]
A[6] = A[5] + A[78]
A[4] = A[6] + A[33]
A[0] = A[3] | A[8]
A[3] = A[2] | A[8]
A[2] = A[1] | A[8]
A[6] = rotl(A[4] | A[8], 20)
A[7] = A[6] + A[1]
A[1] = A[7] | A[8]
A[5] = A[3] & A[1]
A[6] = A[3] ^ A[9]
A[7] = A[6] & A[2]
A[4] = A[5] | A[7]
A[5] = A[4] + A[0]
A[6] = A[5] + A[83]
A[4] = A[6] + A[34]
A[0] = A[3] | A[8]
A[3] = A[2] | A[8]
A[2] = A[1] | A[8]
A[6] = rotl(A[4] | A[8], 5)
A[7] = A[6] + A[1]
A[1] = A[7] | A[8]
A[5] = A[3] & A[1]
A[6] = A[3] ^ A[9]
A[7] = A[6] & A[2]
A[4] = A[5] | A[7]
A[5] = A[4] + A[0]
A[6] = A[5] + A[88]
A[4] = A[6] + A[35]
A[0] = A[3] | A[8]
A[3] = A[2] | A[8]
A[2] = A[1] | A[8]
A[6] = rotl(A[4] | A[8], 9)
A[7] = A[6] + A[1]
A[1] = A[7] | A[8]
A[5] = A[3] & A[1]
A[6] = A[3] ^ A[9]
A[7] = A[6] & A[2]
A[4] = A[5] | A[7]
A[5] = A[4] + A[0]
A[6] = A[5] + A[77]
A[4] = A[6] + A[36]
A[0] = A[3] | A[8]
A[3] = A[2] | A[8]
A[2] = A[1] | A[8]
A[6] = rotl(A[4] | A[8], 14)
A[7] = A[6] + A[1]
A[1] = A[7] | A[8]
A[5] = A[3] & A[1]
A[6] = A[3] ^ A[9]
A[7] = A[6] & A[2]
A[4] = A[5] | A[7]
A[5] = A[4] + A[0]
A[6] = A[5] + A[82]
A[4] = A[6] + A[37]
A[0] = A[3] | A[8]
A[3] = A[2] | A[8]
A[2] = A[1] | A[8]
A[6] = rotl(A[4] | A[8], 20)
A[7] = A[6] + A[1]
A[1] = A[7] | A[8]
A[5] = A[3] & A[1]
A[6] = A[3] ^ A[9]
A[7] = A[6] & A[2]
A[4] = A[5] | A[7]
A[5] = A[4] + A[0]
A[6] = A[5] + A[87]
A[4] = A[6] + A[38]
A[0] = A[3] | A[8]
A[3] = A[2] | A[8]
A[2] = A[1] | A[8]
A[6] = rotl(A[4] | A[8], 5)
A[7] = A[6] + A[1]
A[1] = A[7] | A[8]
A[5] = A[3] & A[1]
A[6] = A[3] ^ A[9]
A[7] = A[6] & A[2]
A[4] = A[5] | A[7]
A[5] = A[4] + A[0]
A[6] = A[5] + A[76]
A[4] = A[6] + A[39]
A[0] = A[3] | A[8]
A[3] = A[2] | A[8]
A[2] = A[1] | A[8]
A[6] = rotl(A[4] | A[8], 9)
A[7] = A[6] + A[1]
A[1] = A[7] | A[8]
A[5] = A[3] & A[1]
A[6] = A[3] ^ A[9]
A[7] = A[6] & A[2]
A[4] = A[5] | A[7]
A[5] = A[4] + A[0]
A[6] = A[5] + A[81]
A[4] = A[6] + A[40]
A[0] = A[3] | A[8]
A[3] = A[2] | A[8]
A[2] = A[1] | A[8]
A[6] = rotl(A[4] | A[8], 14)
A[7] = A[6] + A[1]
A[1] = A[7] | A[8]
A[5] = A[3] & A[1]
A[6] = A[3] ^ A[9]
A[7] = A[6] & A[2]
A[4] = A[5] | A[7]
A[5] = A[4] + A[0]
A[6] = A[5] + A[86]
A[4] = A[6] + A[41]
A[0] = A[3] | A[8]
A[3] = A[2] | A[8]
A[2] = A[1] | A[8]
A[6] = rotl(A[4] | A[8], 20)
A[7] = A[6] + A[1]
A[1] = A[7] | A[8]
A[5] = A[1] ^ A[2]
A[4] = A[5] ^ A[3]
A[5] = A[4] + A[0]
A[6] = A[5] + A[79]
A[4] = A[6] + A[42]
A[0] = A[3] | A[8]
A[3] = A[2] | A[8]
A[2] = A[1] | A[8]
A[6] = rotl(A[4] | A[8], 4)
A[7] = A[6] + A[1]
A[1] = A[7] | A[8]
A[5] = A[1] ^ A[2]
A[4] = A[5] ^ A[3]
A[5] = A[4] + A[0]
A[6] = A[5] + A[82]
A[4] = A[6] + A[43]
A[0] = A[3] | A[8]
A[3] = A[2] | A[8]
A[2] = A[1] | A[8]
A[6] = rotl(A[4] | A[8], 11)
A[7] = A[6] + A[1]
A[1] = A[7] | A[8]
A[5] = A[1] ^ A[2]
A[4] = A[5] ^ A[3]
A[5] = A[4] + A[0]
A[6] = A[5] + A[85]
A[4] = A[6] + A[44]
A[0] = A[3] | A[8]
A[3] = A[2] | A[8]
A[2] = A[1] | A[8]
A[6] = rotl(A[4] | A[8], 16)
A[7] = A[6] + A[1]
A[1] = A[7] | A[8]
A[5] = A[1] ^ A[2]
A[4] = A[5] ^ A[3]
A[5] = A[4] + A[0]
A[6] = A[5] + A[88]
A[4] = A[6] + A[45]
A[0] = A[3] | A[8]
A[3] = A[2] | A[8]
A[2] = A[1] | A[8]
A[6] = rotl(A[4] | A[8], 23)
A[7] = A[6] + A[1]
A[1] = A[7] | A[8]
A[5] = A[1] ^ A[2]
A[4] = A[5] ^ A[3]
A[5] = A[4] + A[0]
A[6] = A[5] + A[75]
A[4] = A[6] + A[46]
A[0] = A[3] | A[8]
A[3] = A[2] | A[8]
A[2] = A[1] | A[8]
A[6] = rotl(A[4] | A[8], 4)
A[7] = A[6] + A[1]
A[1] = A[7] | A[8]
A[5] = A[1] ^ A[2]
A[4] = A[5] ^ A[3]
A[5] = A[4] + A[0]
A[6] = A[5] + A[78]
A[4] = A[6] + A[47]
A[0] = A[3] | A[8]
A[3] = A[2] | A[8]
A[2] = A[1] | A[8]
A[6] = rotl(A[4] | A[8], 11)
A[7] = A[6] + A[1]
A[1] = A[7] | A[8]
A[5] = A[1] ^ A[2]
A[4] = A[5] ^ A[3]
A[5] = A[4] + A[0]
A[6] = A[5] + A[81]
A[4] = A[6] + A[48]
A[0] = A[3] | A[8]
A[3] = A[2] | A[8]
A[2] = A[1] | A[8]
A[6] = rotl(A[4] | A[8], 16)
A[7] = A[6] + A[1]
A[1] = A[7] | A[8]
A[5] = A[1] ^ A[2]
A[4] = A[5] ^ A[3]
A[5] = A[4] + A[0]
A[6] = A[5] + A[84]
A[4] = A[6] + A[49]
A[0] = A[3] | A[8]
A[3] = A[2] | A[8]
A[2] = A[1] | A[8]
A[6] = rotl(A[4] | A[8], 23)
A[7] = A[6] + A[1]
A[1] = A[7] | A[8]
A[5] = A[1] ^ A[2]
A[4] = A[5] ^ A[3]
A[5] = A[4] + A[0]
A[6] = A[5] + A[87]
A[4] = A[6] + A[50]
A[0] = A[3] | A[8]
A[3] = A[2] | A[8]
A[2] = A[1] | A[8]
A[6] = rotl(A[4] | A[8], 4)
A[7] = A[6] + A[1]
A[1] = A[7] | A[8]
A[5] = A[1] ^ A[2]
A[4] = A[5] ^ A[3]
A[5] = A[4] + A[0]
A[6] = A[5] + A[74]
A[4] = A[6] + A[51]
A[0] = A[3] | A[8]
A[3] = A[2] | A[8]
A[2] = A[1] | A[8]
A[6] = rotl(A[4] | A[8], 11)
A[7] = A[6] + A[1]
A[1] = A[7] | A[8]
A[5] = A[1] ^ A[2]
A[4] = A[5] ^ A[3]
A[5] = A[4] + A[0]
A[6] = A[5] + A[77]
A[4] = A[6] + A[52]
A[0] = A[3] | A[8]
A[3] = A[2] | A[8]
A[2] = A[1] | A[8]
A[6] = rotl(A[4] | A[8], 16)
A[7] = A[6] + A[1]
A[1] = A[7] | A[8]
A[5] = A[1] ^ A[2]
A[4] = A[5] ^ A[3]
A[5] = A[4] + A[0]
A[6] = A[5] + A[80]
A[4] = A[6] + A[53]
A[0] = A[3] | A[8]
A[3] = A[2] | A[8]
A[2] = A[1] | A[8]
A[6] = rotl(A[4] | A[8], 23)
A[7] = A[6] + A[1]
A[1] = A[7] | A[8]
A[5] = A[1] ^ A[2]
A[4] = A[5] ^ A[3]
A[5] = A[4] + A[0]
A[6] = A[5] + A[83]
A[4] = A[6] + A[54]
A[0] = A[3] | A[8]
A[3] = A[2] | A[8]
A[2] = A[1] | A[8]
A[6] = rotl(A[4] | A[8], 4)
A[7] = A[6] + A[1]
A[1] = A[7] | A[8]
A[5] = A[1] ^ A[2]
A[4] = A[5] ^ A[3]
A[5] = A[4] + A[0]
A[6] = A[5] + A[86]
A[4] = A[6] + A[55]
A[0] = A[3] | A[8]
A[3] = A[2] | A[8]
A[2] = A[1] | A[8]
A[6] = rotl(A[4] | A[8], 11)
A[7] = A[6] + A[1]
A[1] = A[7] | A[8]
A[5] = A[1] ^ A[2]
A[4] = A[5] ^ A[3]
A[5] = A[4] + A[0]
A[6] = A[5] + A[89]
A[4] = A[6] + A[56]
A[0] = A[3] | A[8]
A[3] = A[2] | A[8]
A[2] = A[1] | A[8]
A[6] = rotl(A[4] | A[8], 16)
A[7] = A[6] + A[1]
A[1] = A[7] | A[8]
A[5] = A[1] ^ A[2]
A[4] = A[5] ^ A[3]
A[5] = A[4] + A[0]
A[6] = A[5] + A[76]
A[4] = A[6] + A[57]
A[0] = A[3] | A[8]
A[3] = A[2] | A[8]
A[2] = A[1] | A[8]
A[6] = rotl(A[4] | A[8], 23)
A[7] = A[6] + A[1]
A[1] = A[7] | A[8]
A[5] = A[3] ^ A[9]
A[6] = A[5] | A[1]
A[4] = A[2] ^ A[6]
A[5] = A[4] + A[0]
A[6] = A[5] + A[74]
A[4] = A[6] + A[58]
A[0] = A[3] | A[8]
A[3] = A[2] | A[8]
A[2] = A[1] | A[8]
A[6] = rotl(A[4] | A[8], 6)
A[7] = A[6] + A[1]
A[1] = A[7] | A[8]
A[5] = A[3] ^ A[9]
A[6] = A[5] | A[1]
A[4] = A[2] ^ A[6]
A[5] = A[4] + A[0]
A[6] = A[5] + A[81]
A[4] = A[6] + A[59]
A[0] = A[3] | A[8]
A[3] = A[2] | A[8]
A[2] = A[1] | A[8]
A[6] = rotl(A[4] | A[8], 10)
A[7] = A[6] + A[1]
A[1] = A[7] | A[8]
A[5] = A[3] ^ A[9]
A[6] = A[5] | A[1]
A[4] = A[2] ^ A[6]
A[5] = A[4] + A[0]
A[6] = A[5] + A[88]
A[4] = A[6] + A[60]
A[0] = A[3] | A[8]
A[3] = A[2] | A[8]
A[2] = A[1] | A[8]
A[6] = rotl(A[4] | A[8], 15)
A[7] = A[6] + A[1]
A[1] = A[7] | A[8]
A[5] = A[3] ^ A[9]
A[6] = A[5] | A[1]
A[4] = A[2] ^ A[6]
A[5] = A[4] + A[0]
A[6] = A[5] + A[79]
A[4] = A[6] + A[61]
A[0] = A[3] | A[8]
A[3] = A[2] | A[8]
A[2] = A[1] | A[8]
A[6] = rotl(A[4] | A[8], 21)
A[7] = A[6] + A[1]
A[1] = A[7] | A[8]
A[5] = A[3] ^ A[9]
A[6] = A[5] | A[1]
A[4] = A[2] ^ A[6]
A[5] = A[4] + A[0]
A[6] = A[5] + A[86]
A[4] = A[6] + A[62]
A[0] = A[3] | A[8]
A[3] = A[2] | A[8]
A[2] = A[1] | A[8]
A[6] = rotl(A[4] | A[8], 6)
A[7] = A[6] + A[1]
A[1] = A[7] | A[8]
A[5] = A[3] ^ A[9]
A[6] = A[5] | A[1]
A[4] = A[2] ^ A[6]
A[5] = A[4] + A[0]
A[6] = A[5] + A[77]
A[4] = A[6] + A[63]
A[0] = A[3] | A[8]
A[3] = A[2] | A[8]
A[2] = A[1] | A[8]
A[6] = rotl(A[4] | A[8], 10)
A[7] = A[6] + A[1]
A[1] = A[7] | A[8]
A[5] = A[3] ^ A[9]
A[6] = A[5] | A[1]
A[4] = A[2] ^ A[6]
A[5] = A[4] + A[0]
A[6] = A[5] + A[84]
A[4] = A[6] + A[64]
A[0] = A[3] | A[8]
A[3] = A[2] | A[8]
A[2] = A[1] | A[8]
A[6] = rotl(A[4] | A[8], 15)
A[7] = A[6] + A[1]
A[1] = A[7] | A[8]
A[5] = A[3] ^ A[9]
A[6] = A[5] | A[1]
A[4] = A[2] ^ A[6]
A[5] = A[4] + A[0]
A[6] = A[5] + A[75]
A[4] = A[6] + A[65]
A[0] = A[3] | A[8]
A[3] = A[2] | A[8]
A[2] = A[1] | A[8]
A[6] = rotl(A[4] | A[8], 21)
A[7] = A[6] + A[1]
A[1] = A[7] | A[8]
A[5] = A[3] ^ A[9]
A[6] = A[5] | A[1]
A[4] = A[2] ^ A[6]
A[5] = A[4] + A[0]
A[6] = A[5] + A[82]
A[4] = A[6] + A[66]
A[0] = A[3] | A[8]
A[3] = A[2] | A[8]
A[2] = A[1] | A[8]
A[6] = rotl(A[4] | A[8], 6)
A[7] = A[6] + A[1]
A[1] = A[7] | A[8]
A[5] = A[3] ^ A[9]
A[6] = A[5] | A[1]
A[4] = A[2] ^ A[6]
A[5] = A[4] + A[0]
A[6] = A[5] + A[89]
A[4] = A[6] + A[67]
A[0] = A[3] | A[8]
A[3] = A[2] | A[8]
A[2] = A[1] | A[8]
A[6] = rotl(A[4] | A[8], 10)
A[7] = A[6] + A[1]
A[1] = A[7] | A[8]
A[5] = A[3] ^ A[9]
A[6] = A[5] | A[1]
A[4] = A[2] ^ A[6]
A[5] = A[4] + A[0]
A[6] = A[5] + A[80]
A[4] = A[6] + A[68]
A[0] = A[3] | A[8]
A[3] = A[2] | A[8]
A[2] = A[1] | A[8]
A[6] = rotl(A[4] | A[8], 15)
A[7] = A[6] + A[1]
A[1] = A[7] | A[8]
A[5] = A[3] ^ A[9]
A[6] = A[5] | A[1]
A[4] = A[2] ^ A[6]
A[5] = A[4] + A[0]
A[6] = A[5] + A[87]
A[4] = A[6] + A[69]
A[0] = A[3] | A[8]
A[3] = A[2] | A[8]
A[2] = A[1] | A[8]
A[6] = rotl(A[4] | A[8], 21)
A[7] = A[6] + A[1]
A[1] = A[7] | A[8]
A[5] = A[3] ^ A[9]
A[6] = A[5] | A[1]
A[4] = A[2] ^ A[6]
A[5] = A[4] + A[0]
A[6] = A[5] + A[78]
A[4] = A[6] + A[70]
A[0] = A[3] | A[8]
A[3] = A[2] | A[8]
A[2] = A[1] | A[8]
A[6] = rotl(A[4] | A[8], 6)
A[7] = A[6] + A[1]
A[1] = A[7] | A[8]
A[5] = A[3] ^ A[9]
A[6] = A[5] | A[1]
A[4] = A[2] ^ A[6]
A[5] = A[4] + A[0]
A[6] = A[5] + A[85]
A[4] = A[6] + A[71]
A[0] = A[3] | A[8]
A[3] = A[2] | A[8]
A[2] = A[1] | A[8]
A[6] = rotl(A[4] | A[8], 10)
A[7] = A[6] + A[1]
A[1] = A[7] | A[8]
A[5] = A[3] ^ A[9]
A[6] = A[5] | A[1]
A[4] = A[2] ^ A[6]
A[5] = A[4] + A[0]
A[6] = A[5] + A[76]
A[4] = A[6] + A[72]
A[0] = A[3] | A[8]
A[3] = A[2] | A[8]
A[2] = A[1] | A[8]
A[6] = rotl(A[4] | A[8], 15)
A[7] = A[6] + A[1]
A[1] = A[7] | A[8]
A[5] = A[3] ^ A[9]
A[6] = A[5] | A[1]
A[4] = A[2] ^ A[6]
A[5] = A[4] + A[0]
A[6] = A[5] + A[83]
A[4] = A[6] + A[73]
A[0] = A[3] | A[8]
A[3] = A[2] | A[8]
A[2] = A[1] | A[8]
A[6] = rotl(A[4] | A[8], 21)
A[7] = A[6] + A[1]
A[1] = A[7] | A[8]
A[5] = A[125] + A[0]
A[0] = A[5] | A[8]
A[5] = A[126] + A[1]
A[1] = A[5] | A[8]
A[5] = A[127] + A[2]
A[2] = A[5] | A[8]
A[5] = A[128] + A[3]
A[3] = A[5] | A[8]
Failing with z3
The last thing to do now was to pass everything into z3, and boom get the flag… right? Well, it turned out not to be that simple. I had z3 running for a half an hour but still no output, so what was going on?
I went back to the Ghidra decompilation for any clues to make it go faster. Apparently, I had missed
something; a reference to __ctype_b_loc() in the code. __ctype_b_loc() is a libc function that
is used in the implementations of certain C functions like isalpha() and isdigit(). More
specifically, it returns a const unsigned short int* ctype_b_values[] where each entry contains a
16-bit bitmask in which the nth bit encodes the return value of one of the is*****() functions.
Where is this used, you may ask? After the long stream of if statements, the program iterates
through each byte of the flag (inside corctf{...}), and terminates the loop early if
(ctype_b_values[flag[i]] & 8) == 0. The 3rd bit corresponds to isalnum(), and a set bit means
that the byte is alphanumeric. Therefore, the flag has to be alphanumeric.
I applied this new constraint to z3 hoping it would output a solution this time, but was gutted to find that it still, would not budge.
However, this presents some new useful information; the brute force calculation is not
69,833,729,609,375, but 50*62^6 = 2,840,011,779,200. That’s nearly a 25x improvement, but still
no easy task. Even if each of the 865 instructions I would have to execute accounted for one clock
cycle, it would still take 2,840,011,779,200 * 865 / (2*10^9) / 60 / 60 ~ 341 hours on a typical 2
GHz computer.
At this point we had 14 hours left to the CTF, and it was also 3AM so I wanted to go to sleep. As one final effort for the night, I Googled one of the mysterious hexadecimal constants in the code to see if anything would pop up.
I wasn’t expecting any results, until I started seeing MD5 pop
up! Could it be that this entire program was implementing MD5? Indeed after testing the program with
different inputs, it was in fact MD5, but not entirely. Normally, the MD5 state is initialized to
0x67452301, 0xefcdab89, 0x98badcfe, 0x10325476, but in the program these are all set to zero.
Let’s just call this variant MD5-0.
In any case, I went to sleep with this knowledge hoping to crack this the next day.
The next day
(I woke up bright and early at 11AM the next morning)
Since no
preimage attack on MD5 is known, the only option was to
brute force MD5-0 over 2,840,011,779,200 possibilities, where the correct flag should produce a
suffix of 19c603ba14353ce4.
To test the feasibility of the brute force, I grabbed an online C
implementation of MD5 and measured its
speed. The baseline single-threaded performance on my machine reached around 8*10^6 hashes per second. While this seemed relatively fast to me, the actual running time on 4 cores would be a
daunting 2,840,011,779,200 / (8*10^6) / 60 / 60 / 4 ~ 25 hours.
Optimizing the program by making use of the fact that the flag was always 11 bytes long and
unrolling all of the loops, I was still only able to reach 1.3*10^7 hashes per second, or
15 hours. Still not nearly fast enough!
Vectorization is OP
A common “cheat” to magically increase a program’s speed is by using x86 SIMD instructions to perform
vectorized operations on more than 64 bits at a time. Luckily, my computer supported AVX-512, an
instruction set that allows performing 16 32-bit operations in parallel.
I wrote a new MD5 implementation from scratch utilizing these instructions called md5_avx512, which
could hash 16 11-byte strings. I was expecting maybe a 4-8x speedup, but it ended up being able to
computer hashes 16x faster, which is the theoretical optimum! This brought the estimated time to
just under an hour, which might just be fast enough.
By the time I finished writing the program, we only had one hour left on the clock. Regardless, I ran the program and waited for a miracle. Unfortunately, it took longer than expected, as it had only reached halfway done with only 10 minutes left on the clock. I held out for a clutch victory, but it did not come.
Two stupid bugs
After the CTF concluded I kept my program running, but it actually finished without finding any
solution! To my (annoyed) disbelief, I ended up making two stupid bugs. One of which was using the
flipped endianness for the target suffix, and the other was applying #pragma omp parallel for
without realizing that it was overwriting variables between threads!
After fixing these bugs, I was at last able to run the multi-threaded, AVX-512 optimized MD5-0 brute forcer without any issues:
// gcc -O3 -march=native -o brute brute.c && ./brute
#include <immintrin.h>
#include <pthread.h>
#include <stdio.h>
#include <stdint.h>
#include <string.h>
#define AVX512_F 0xca
#define AVX512_G 0xe4
#define AVX512_H 0x96
#define AVX512_I 0x39
#define AVX512_STEP(f, a, b, c, d, r, k) { \
(a) = _mm512_add_epi32((a), _mm512_add_epi32(_mm512_ternarylogic_epi32((b), (c), (d), (f)), (k))); \
(a) = _mm512_add_epi32(_mm512_rol_epi32((a), (r)), (b)); \
}
#define T0 0xba03c619
#define T1 0xe43c3514
static uint32_t md5_avx512(__m512i x0, __m512i x1, __m512i x2) {
__m512i a = _mm512_setzero_si512();
__m512i b = _mm512_setzero_si512();
__m512i c = _mm512_setzero_si512();
__m512i d = _mm512_setzero_si512();
// Round 1
AVX512_STEP(AVX512_F, a, b, c, d, 7, _mm512_add_epi32(x0, _mm512_set1_epi32(0xd76aa478)));
AVX512_STEP(AVX512_F, d, a, b, c, 12, _mm512_add_epi32(x1, _mm512_set1_epi32(0xe8c7b756)));
AVX512_STEP(AVX512_F, c, d, a, b, 17, _mm512_add_epi32(x2, _mm512_set1_epi32(0x242070db)));
AVX512_STEP(AVX512_F, b, c, d, a, 22, _mm512_set1_epi32(0xc1bdceee));
AVX512_STEP(AVX512_F, a, b, c, d, 7, _mm512_set1_epi32(0xf57c0faf));
AVX512_STEP(AVX512_F, d, a, b, c, 12, _mm512_set1_epi32(0x4787c62a));
AVX512_STEP(AVX512_F, c, d, a, b, 17, _mm512_set1_epi32(0xa8304613));
AVX512_STEP(AVX512_F, b, c, d, a, 22, _mm512_set1_epi32(0xfd469501));
AVX512_STEP(AVX512_F, a, b, c, d, 7, _mm512_set1_epi32(0x698098d8));
AVX512_STEP(AVX512_F, d, a, b, c, 12, _mm512_set1_epi32(0x8b44f7af));
AVX512_STEP(AVX512_F, c, d, a, b, 17, _mm512_set1_epi32(0xffff5bb1));
AVX512_STEP(AVX512_F, b, c, d, a, 22, _mm512_set1_epi32(0x895cd7be));
AVX512_STEP(AVX512_F, a, b, c, d, 7, _mm512_set1_epi32(0x6b901122));
AVX512_STEP(AVX512_F, d, a, b, c, 12, _mm512_set1_epi32(0xfd987193));
AVX512_STEP(AVX512_F, c, d, a, b, 17, _mm512_set1_epi32(0xa67943e6));
AVX512_STEP(AVX512_F, b, c, d, a, 22, _mm512_set1_epi32(0x49b40821));
// Round 2
AVX512_STEP(AVX512_G, a, b, c, d, 5, _mm512_add_epi32(x1, _mm512_set1_epi32(0xf61e2562)));
AVX512_STEP(AVX512_G, d, a, b, c, 9, _mm512_set1_epi32(0xc040b340));
AVX512_STEP(AVX512_G, c, d, a, b, 14, _mm512_set1_epi32(0x265e5a51));
AVX512_STEP(AVX512_G, b, c, d, a, 20, _mm512_add_epi32(x0, _mm512_set1_epi32(0xe9b6c7aa)));
AVX512_STEP(AVX512_G, a, b, c, d, 5, _mm512_set1_epi32(0xd62f105d));
AVX512_STEP(AVX512_G, d, a, b, c, 9, _mm512_set1_epi32(0x02441453));
AVX512_STEP(AVX512_G, c, d, a, b, 14, _mm512_set1_epi32(0xd8a1e681));
AVX512_STEP(AVX512_G, b, c, d, a, 20, _mm512_set1_epi32(0xe7d3fbc8));
AVX512_STEP(AVX512_G, a, b, c, d, 5, _mm512_set1_epi32(0x21e1cde6));
AVX512_STEP(AVX512_G, d, a, b, c, 9, _mm512_set1_epi32(0xc337082e));
AVX512_STEP(AVX512_G, c, d, a, b, 14, _mm512_set1_epi32(0xf4d50d87));
AVX512_STEP(AVX512_G, b, c, d, a, 20, _mm512_set1_epi32(0x455a14ed));
AVX512_STEP(AVX512_G, a, b, c, d, 5, _mm512_set1_epi32(0xa9e3e905));
AVX512_STEP(AVX512_G, d, a, b, c, 9, _mm512_add_epi32(x2, _mm512_set1_epi32(0xfcefa3f8)));
AVX512_STEP(AVX512_G, c, d, a, b, 14, _mm512_set1_epi32(0x676f02d9));
AVX512_STEP(AVX512_G, b, c, d, a, 20, _mm512_set1_epi32(0x8d2a4c8a));
// Round 3
AVX512_STEP(AVX512_H, a, b, c, d, 4, _mm512_set1_epi32(0xfffa3942));
AVX512_STEP(AVX512_H, d, a, b, c, 11, _mm512_set1_epi32(0x8771f681));
AVX512_STEP(AVX512_H, c, d, a, b, 16, _mm512_set1_epi32(0x6d9d6122));
AVX512_STEP(AVX512_H, b, c, d, a, 23, _mm512_set1_epi32(0xfde53864));
AVX512_STEP(AVX512_H, a, b, c, d, 4, _mm512_add_epi32(x1, _mm512_set1_epi32(0xa4beea44)));
AVX512_STEP(AVX512_H, d, a, b, c, 11, _mm512_set1_epi32(0x4bdecfa9));
AVX512_STEP(AVX512_H, c, d, a, b, 16, _mm512_set1_epi32(0xf6bb4b60));
AVX512_STEP(AVX512_H, b, c, d, a, 23, _mm512_set1_epi32(0xbebfbc70));
AVX512_STEP(AVX512_H, a, b, c, d, 4, _mm512_set1_epi32(0x289b7ec6));
AVX512_STEP(AVX512_H, d, a, b, c, 11, _mm512_add_epi32(x0, _mm512_set1_epi32(0xeaa127fa)));
AVX512_STEP(AVX512_H, c, d, a, b, 16, _mm512_set1_epi32(0xd4ef3085));
AVX512_STEP(AVX512_H, b, c, d, a, 23, _mm512_set1_epi32(0x04881d05));
AVX512_STEP(AVX512_H, a, b, c, d, 4, _mm512_set1_epi32(0xd9d4d039));
AVX512_STEP(AVX512_H, d, a, b, c, 11, _mm512_set1_epi32(0xe6db99e5));
AVX512_STEP(AVX512_H, c, d, a, b, 16, _mm512_set1_epi32(0x1fa27cf8));
AVX512_STEP(AVX512_H, b, c, d, a, 23, _mm512_add_epi32(x2, _mm512_set1_epi32(0xc4ac5665)));
// Round 4
AVX512_STEP(AVX512_I, a, b, c, d, 6, _mm512_add_epi32(x0, _mm512_set1_epi32(0xf4292244)));
AVX512_STEP(AVX512_I, d, a, b, c, 10, _mm512_set1_epi32(0x432aff97));
AVX512_STEP(AVX512_I, c, d, a, b, 15, _mm512_set1_epi32(0xab9423ff));
AVX512_STEP(AVX512_I, b, c, d, a, 21, _mm512_set1_epi32(0xfc93a039));
AVX512_STEP(AVX512_I, a, b, c, d, 6, _mm512_set1_epi32(0x655b59c3));
AVX512_STEP(AVX512_I, d, a, b, c, 10, _mm512_set1_epi32(0x8f0ccc92));
AVX512_STEP(AVX512_I, c, d, a, b, 15, _mm512_set1_epi32(0xffeff47d));
AVX512_STEP(AVX512_I, b, c, d, a, 21, _mm512_add_epi32(x1, _mm512_set1_epi32(0x85845dd1)));
AVX512_STEP(AVX512_I, a, b, c, d, 6, _mm512_set1_epi32(0x6fa87e4f));
AVX512_STEP(AVX512_I, d, a, b, c, 10, _mm512_set1_epi32(0xfe2ce6e0));
AVX512_STEP(AVX512_I, c, d, a, b, 15, _mm512_set1_epi32(0xa3014314));
AVX512_STEP(AVX512_I, b, c, d, a, 21, _mm512_set1_epi32(0x4e0811a1));
AVX512_STEP(AVX512_I, a, b, c, d, 6, _mm512_set1_epi32(0xf7537e82));
AVX512_STEP(AVX512_I, d, a, b, c, 10, _mm512_set1_epi32(0xbd3af235));
AVX512_STEP(AVX512_I, c, d, a, b, 15, _mm512_add_epi32(x2, _mm512_set1_epi32(0x2ad7d2bb)));
AVX512_STEP(AVX512_I, b, c, d, a, 21, _mm512_set1_epi32(0xeb86d391));
__mmask16 eq_c = _mm512_cmpeq_epi32_mask(c, _mm512_set1_epi32(T0));
__mmask16 eq_d = _mm512_cmpeq_epi32_mask(d, _mm512_set1_epi32(T1));
__mmask16 eq = eq_c & eq_d;
if (eq) {
__attribute__((aligned(64))) uint32_t _x0[16], _x1[16], _x2[16];
_mm512_store_si512(_x0, x0);
_mm512_store_si512(_x1, x1);
_mm512_store_si512(_x2, x2);
for (int i = 0; i < 16; i++)
if ((eq >> i) & 1)
printf("found: %.4s%.4s%.4s\n", (uint8_t *)&_x0[i], (uint8_t *)&_x1[i], (uint8_t *)&_x2[i]);
}
}
#define A 62
#define NTHREADS 8
const char ALPHABET[64] = "0123456789ABCDEFGHIJKLMNOPQRSTUVWXYZabcdefghijklmnopqrstuvwxyz00";
const char ALPHABET_S4[50] = "012345ABCDEFGHIJKLMNOPQRSTUVabcdefghijklmnopqrstuv";
static void *search(void *arg) {
__attribute__((aligned(64))) uint32_t _x0[16], _x1[16], _x2[16];
int n = (uint64_t)arg;
int start = n * (50 / NTHREADS);
int end = n != NTHREADS - 1 ? (n + 1) * (50 / NTHREADS) : 50;
printf("starting search [%d, %d)\n", start, end);
uint8_t flag[12] = { 0 };
flag[11] = 0x80;
const __m512i Y0 = _mm512_setr_epi32(48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 65, 66, 67, 68, 69, 70);
const __m512i Y1 = _mm512_setr_epi32(71, 72, 73, 74, 75, 76, 77, 78, 79, 80, 81, 82, 83, 84, 85, 86);
const __m512i Y2 = _mm512_setr_epi32(87, 88, 89, 90, 97, 98, 99, 100, 101, 102, 103, 104, 105, 106, 107, 108);
const __m512i Y3 = _mm512_setr_epi32(109, 110, 111, 112, 113, 114, 115, 116, 117, 118, 119, 120, 121, 122, 48, 48);
for (int c0 = start; c0 < end; c0++) {
flag[9] = ALPHABET_S4[c0];
flag[0] = ALPHABET_S4[c0] + 1;
flag[7] = ALPHABET_S4[c0] + 4;
for (int c1 = 0; c1 < A; c1++) {
flag[1] = flag[10] = ALPHABET[c1];
for (int c2 = 0; c2 < A; c2++) {
flag[2] = flag[4] = ALPHABET[c2];
for (int c3 = 0; c3 < A; c3++) {
flag[3] = ALPHABET[c3];
for (int c4 = 0; c4 < A; c4++) {
flag[5] = ALPHABET[c4];
for (int c5 = 0; c5 < A; c5++) {
flag[6] = ALPHABET[c5];
uint32_t *flag_u32 = (uint32_t *)flag;
for (int i = 0; i < 16; i++) {
_x0[i] = flag_u32[0];
_x1[i] = flag_u32[1];
_x2[i] = flag_u32[2];
}
__m512i x0 = _mm512_load_si512(_x0);
__m512i x1 = _mm512_load_si512(_x1);
__m512i x2 = _mm512_load_si512(_x2);
md5_avx512(x0, x1, _mm512_or_si512(x2, Y0));
md5_avx512(x0, x1, _mm512_or_si512(x2, Y1));
md5_avx512(x0, x1, _mm512_or_si512(x2, Y2));
md5_avx512(x0, x1, _mm512_or_si512(x2, Y3));
}
}
}
}
}
printf("checkpoint: %d (thread %d)\n", c0, n);
}
}
int main() {
pthread_t threads[NTHREADS];
for (uint64_t i = 0; i < NTHREADS; i++)
pthread_create(&threads[i], NULL, search, (void *)i);
for (uint64_t i = 0; i < NTHREADS; i++)
pthread_join(threads[i], NULL);
return 0;
}
1hr 20mins later, it found the flag: corctf{cPv3v8VfWbP}. The full flag emerges when it is
submitted to digestme:
$ ./digestme
Welcome!
Please enter the flag here:
corctf{cPv3v8VfWbP}
Nice!
Full flag: corctf{youtu.be/dQw4w9WgXcQ}
Final thoughts
Despite being so close to solving it in the end – and also costing us 6th place, I enjoyed every part of the challenge, from converting the disassembly into bitwise operations and then 32-bit integer arithmetic, to realizing it was MD5 all along, and even writing the bruteforcer that I somehow messed up.
I do believe the challenge would have been better off with a smaller search space, because some people (like me) don’t have strong CPUs or GPUs. On the other hand, I think performance optimization is fun, especially when SIMD is involved.

