Challenge

Any technology that is advanced enough is indistinguishable from magic. This binary does it next level: it is magic raised to the third power.

Connect via

nc magic3.sdc.tf 1337

Binary

magic3

By k3v1n

• Solves: 9
• Points: 450
• Category: Reversing (“Revenge” as called in the CTF)
  
  
  

Part 1: Reversing

By desp

Magic is but an illusion

Advanced technology might be indistinguishable from magic on the surface, but as a CTF team, we cannot settle with that notion - time to investigate how magical it truly is! Opening it up in IDA, we are greeted with quite a standard decompilation:

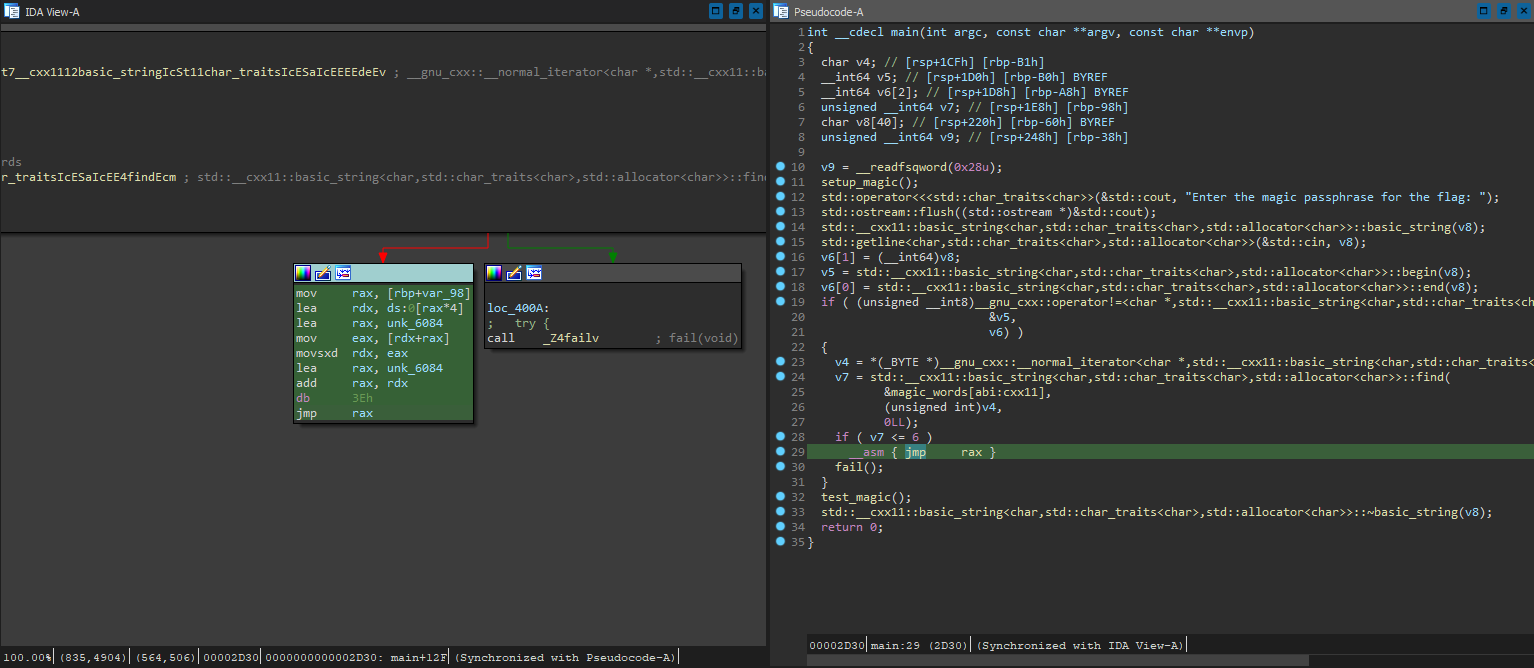
Looks like we are dealing with C++ here, with the amount of demangled functions. Nothing out of the ordinary here - aside from a weird _asm call to jmp rax. Looks like IDA failed to construct a jump table correctly again; Let’s give it a helping hand by manually defining the switch using Other -> Specify switch idiom, and specifying the jump table according to the data at 0x6084:

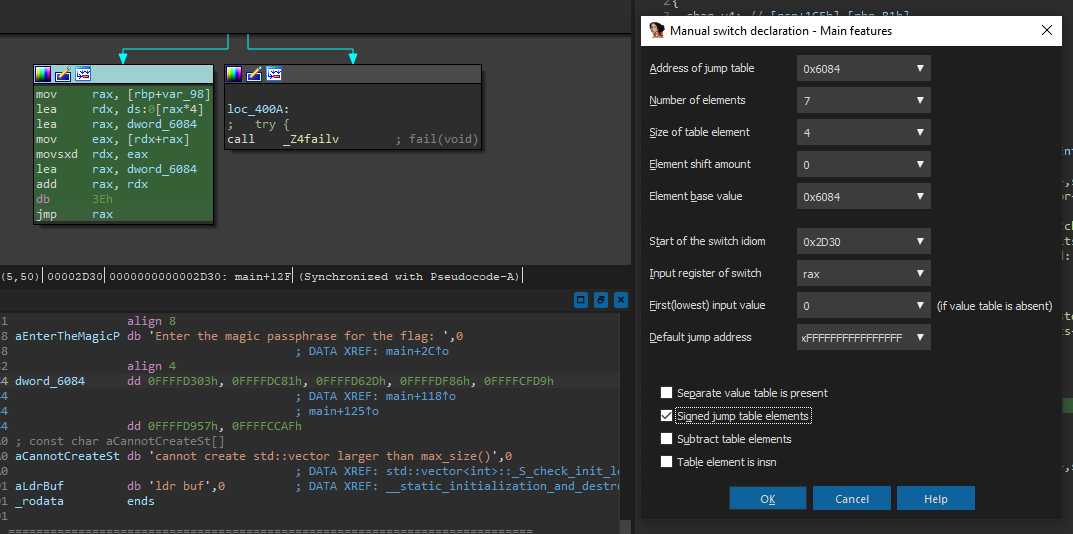
Don’t forget to tick the Signed jump table elements - the data at unk_6084 (now dword_6084 since we defined the array type) aren’t pointers but integers, which is evident by the sign extended hex FFFF**** that signifies the elements are all negative offsets. Let’s check what we have now:

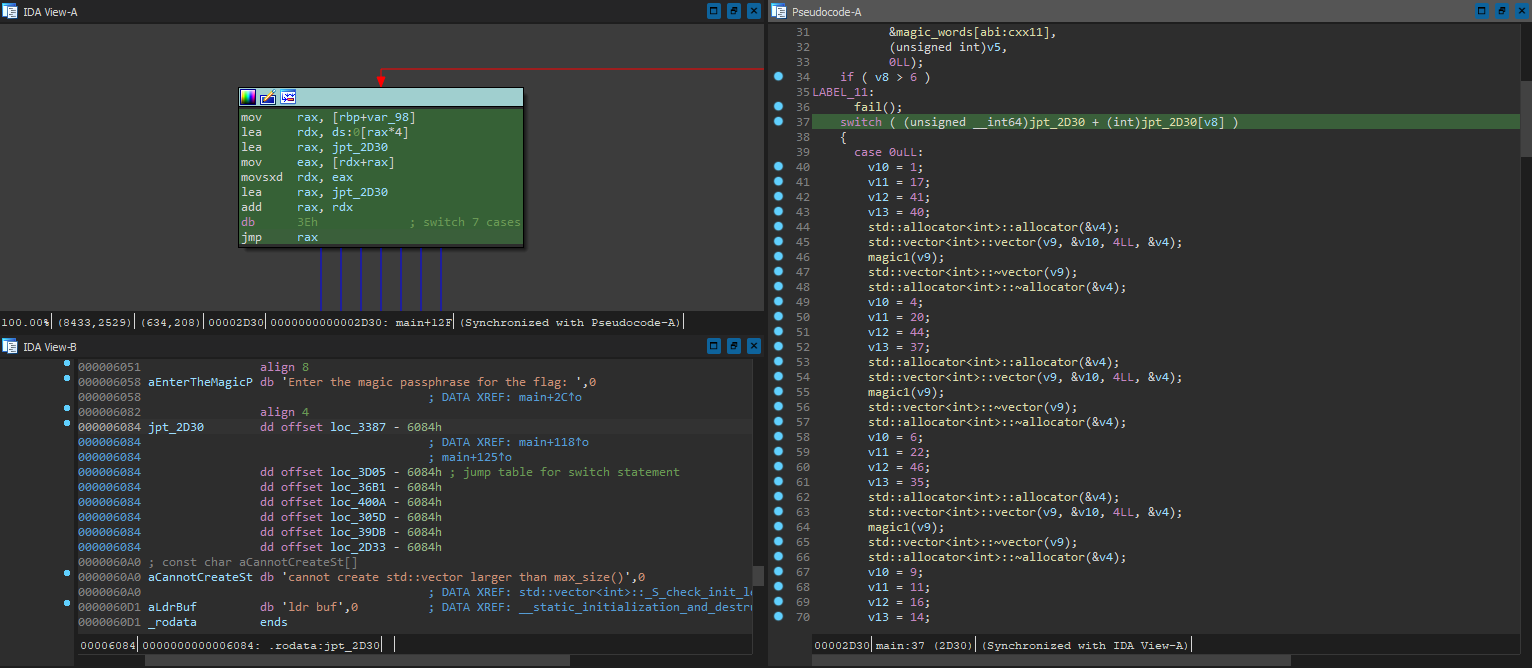
Nice! It’s now showing what all the branches are doing in the decompilation. Ignoring the C++ boilerplates, it looks like aside from case 3 which jumps to fail() instantly, all 6 of the rest of the cases set some integer values before calling magic1, repeating this process 5 times in total. After poking around for a while, we can already reason about what the program is doing on the high level:

• Before main, a static initializer _GLOBAL__sub_I__Z11magic_wordsB5cxx11 is run by _libc_csu_init, which sets magic_word to the string ldr buf.
• Once in main, it first calls setup_magic(), which sets up magic_array with consecutive integers with std::iota, then issues multiple calls to magic1 with quite a bit of integers passed to it.
• It then accepts 1 line of input with no length limit that matches any character in magic_word, maps the characters to the cases (aside from the space), and process it by calling magic1 5 times with the integer parameters set before each call.
• Finally, it calls test_magic which iterates over the magic_array, printing the flag after asserting that magic_array consists of only ascending consecutive integers, just like the original state right after std::iota.

The only piece of the puzzle left now is to figure out what magic1 is doing. Turns out, it is also quite straightforward:

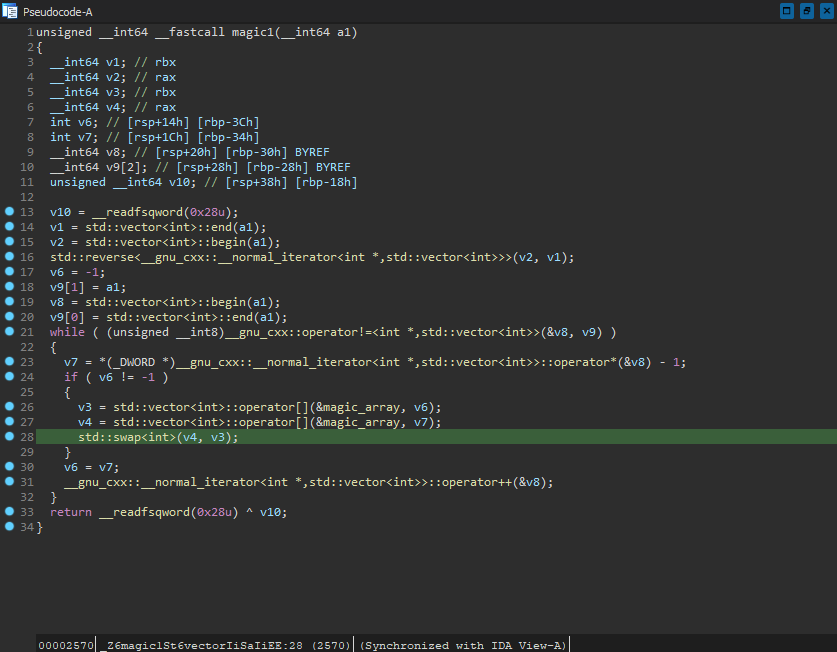
It loops over the values passed to the function, utilizing the values as indexes to pairwise swap the elements in magic_array. Note that it loops the indexes from the bottom up when considering the order shown in the decompilation - this is due to the call to std::reverse. Considering how simple this entire program is, why is it called magic, and to the extent of a cube even?

Magic-ematics

What’s a better way to verify whether we’ve analyzed correctly than to reimplement the algorithm in a more readable language? With some quick scripting, we can obtain something like this:

import itertools
import sys

#after setup_magic
magic = [
40, 25, 29, 46, 27, 45, 33, 34,
15, 38, 13, 3, 12, 18, 11, 47,
39, 1, 8, 19, 28, 31, 30, 32,
0, 20, 23, 35, 14, 26, 17, 16,
42, 4, 21, 43, 9, 10, 41, 24,
37, 44, 2, 36, 6, 7, 22, 5
]

def pairwise(iterable):
    a, b = itertools.tee(iterable)
    next(b, None)
    return zip(a, b)

def swapall(arr, indexes):
    for i, j in pairwise(indexes[::-1]):  #reverse the indexes as noted in the above section
        arr[i-1], arr[j-1] = arr[j-1], arr[i-1]

# accepts argument as input
test = sys.argv[1] if len(sys.argv) > 1 else ''

def l(na):
    swapall(na, [1, 17, 41, 40])
    swapall(na, [4, 20, 44, 37])
    swapall(na, [6, 22, 46, 35])
    swapall(na, [9, 11, 16, 14])
    swapall(na, [10, 13, 15, 12])

def d(na):
    swapall(na, [14, 22, 30, 38])
    swapall(na, [15, 23, 31, 39])
    swapall(na, [16, 24, 32, 40])
    swapall(na, [41, 43, 48, 46])
    swapall(na, [42, 45, 47, 44])

def r(na):
    swapall(na, [3, 38, 43, 19])
    swapall(na, [5, 36, 45, 21])
    swapall(na, [8, 33, 48, 24])
    swapall(na, [25, 27, 32, 30])
    swapall(na, [26, 29, 31, 28])

def b(na):
    swapall(na, [1, 14, 48, 27])
    swapall(na, [2, 12, 47, 29])
    swapall(na, [3, 9, 46, 32])
    swapall(na, [33, 35, 40, 38])
    swapall(na, [34, 37, 39, 36])

def u(na):
    swapall(na, [1, 3, 8, 6])
    swapall(na, [2, 5, 7, 4])
    swapall(na, [9, 33, 25, 17])
    swapall(na, [10, 34, 26, 18])
    swapall(na, [11, 35, 27, 19])

def f(na):
    swapall(na, [6, 25, 43, 16])
    swapall(na, [7, 28, 42, 13])
    swapall(na, [8, 30, 41, 11])
    swapall(na, [17, 19, 24, 22])
    swapall(na, [18, 21, 23, 20])

jpt = {'l': l, 'd': d, 'r': r, 'b': b, 'u': u, 'f': f}

for c in test:
    jpt[c](magic)

print(", ".join([str(i+1) + ":" + str(v) for i,v in enumerate(magic)]))

With some help of a native debugger and some breakpoints before test_magic, we can verify that their outputs do indeed match. However, after staring at it for quite a while, it still didn’t seem like there is any pattern that we can identify - the values all seem quite arbitrary. Guess we might as well write a brute force script to run in the background while we figure the logic out:

import java.time.OffsetDateTime;
import java.time.format.DateTimeFormatter;
import java.util.Arrays;
import java.util.concurrent.CompletableFuture;
import java.util.concurrent.Executors;
import java.util.concurrent.ForkJoinPool;
import java.util.concurrent.TimeUnit;

public class DeMagic {

    private static ForkJoinPool ex = new ForkJoinPool(28);

    private static int[] magic = {
    40, 25, 29, 46, 27, 45, 33, 34,
    15, 38, 13, 3, 12, 18, 11, 47,
    39, 1, 8, 19, 28, 31, 30, 32,
    0, 20, 23, 35, 14, 26, 17, 16,
    42, 4, 21, 43, 9, 10, 41, 24,
    37, 44, 2, 36, 6, 7, 22, 5
    };

    private static void swapall(int[] arr, int[] indexes) {
        for(int i = indexes.length - 1; i >= 0; i--) {
            int temp = arr[indexes[i]-1];
            arr[indexes[i]-1] = arr[indexes[i+1]-1];
            arr[indexes[i+1]-1] = temp;
        }
    }

    private static boolean checkSorted(int[] arr, int length) {
        for(int i = 0; i < length - 1; i++) {
            if(arr[i] + 1 != arr[i]) return false;
        }
        return true;
    }

    private static void search(int step, int sorted, String path, int[] arr) {

        if(checkSorted(arr, arr.length)) {
            System.out.println(path);
            System.exit(0);
        }

        if(step >= (sorted + 1) * 5) {
            System.out.println("terminating branch " + step + " " + sorted + " " + path);
            return;
        }

        final int s = step + 1;

        int[] na1 = Arrays.copyOf(arr, 48);
        swapall(na1, new int[] {1, 17, 41, 40});
        swapall(na1, new int[] {4, 20, 44, 37});
        swapall(na1, new int[] {6, 22, 46, 35});
        swapall(na1, new int[] {9, 11, 16, 14});
        swapall(na1, new int[] {10, 13, 15, 12});
        if(checkSorted(na1, sorted))
            CompletableFuture.runAsync(() -> search(s, sorted + (na1[sorted] + 1 == na1[sorted+1] ? 1 : 0), path+'l', na1), ex);

        int[] na2 = Arrays.copyOf(arr, 48);
        swapall(na2, new int[] {14, 22, 30, 38});
        swapall(na2, new int[] {15, 23, 31, 39});
        swapall(na2, new int[] {16, 24, 32, 40});
        swapall(na2, new int[] {41, 43, 48, 46});
        swapall(na2, new int[] {42, 45, 47, 44});
        if(checkSorted(na2, sorted))
            CompletableFuture.runAsync(() -> search(s, sorted + (na2[sorted] + 1 == na2[sorted+1] ? 1 : 0), path+'d', na2), ex);

        int[] na3 = Arrays.copyOf(arr, 48);
        swapall(na3, new int[] {3, 38, 43, 19});
        swapall(na3, new int[] {5, 36, 45, 21});
        swapall(na3, new int[] {8, 33, 48, 24});
        swapall(na3, new int[] {25, 27, 32, 30});
        swapall(na3, new int[] {26, 29, 31, 28});
        if(checkSorted(na3, sorted))
            CompletableFuture.runAsync(() -> search(s, sorted + (na3[sorted] + 1 == na3[sorted+1] ? 1 : 0), path+'r', na3), ex);

        int[] na4 = Arrays.copyOf(arr, 48);
        swapall(na4, new int[] {1, 14, 48, 27});
        swapall(na4, new int[] {2, 12, 47, 29});
        swapall(na4, new int[] {3, 9, 46, 32});
        swapall(na4, new int[] {33, 35, 40, 38});
        swapall(na4, new int[] {34, 37, 39, 36});
        if(checkSorted(na4, sorted))
            CompletableFuture.runAsync(() -> search(s, sorted + (na4[sorted] + 1 == na4[sorted+1] ? 1 : 0), path+'b', na4), ex);

        int[] na5 = Arrays.copyOf(arr, 48);
        swapall(na5, new int[] {1, 3, 8, 6});
        swapall(na5, new int[] {2, 5, 7, 4});
        swapall(na5, new int[] {9, 33, 25, 17});
        swapall(na5, new int[] {10, 34, 26, 18});
        swapall(na5, new int[] {11, 35, 27, 19});
        if(checkSorted(na5, sorted))
            CompletableFuture.runAsync(() -> search(s, sorted + (na5[sorted] + 1 == na5[sorted+1] ? 1 : 0), path+'u', na5), ex);

        int[] na6 = Arrays.copyOf(arr, 48);
        swapall(na6, new int[] {6, 25, 43, 16});
        swapall(na6, new int[] {7, 28, 42, 13});
        swapall(na6, new int[] {8, 30, 41, 11});
        swapall(na6, new int[] {17, 19, 24, 22});
        swapall(na6, new int[] {18, 21, 23, 20});
        if(checkSorted(na6, sorted))
            CompletableFuture.runAsync(() -> search(s, sorted + (na6[sorted] + 1 == na6[sorted+1] ? 1 : 0), path+'f', na6), ex);
    }

    public static void main(String[] args) {
        search(0, 0, "", magic);

        while(ex.getActiveThreadCount() != 0) {
            try {
                ex.awaitTermination(10, TimeUnit.MINUTES);
            } catch(InterruptedException e) {
                ;
            }
            System.out.println(OffsetDateTime.now().format(DateTimeFormatter.RFC_1123_DATE_TIME) + ": " + ex.getQueuedTaskCount() + " remaining tasks");
        }
    }
}

Yep, it is in java - maybe it’s just me, but multithreading just feels so much easier with java compared to python. Ignoring the inherently roughly coded nature of the script due to direct translation from python (who doesn’t like copy-pasted codes though), quite a bit of assumptions were made in order to cut the search time much shorter:

• There exists a way to sort the array from the first index up without rescrambling it, and
• There exists a way to sort 1 more element in 5 steps or less.

Although they were based on how sorting algorithms work, it was still somewhat questionable - clearly what the algorithm was doing was not some simple sorting, but we have no better methods to base it off on as we have no bounds on bruteforcing otherwise (the input length is unlimited).

In the meantime, let’s investigate deeper into the logic using graph theory! Ok, not really - we will only be visualizing the interactions with graphs instead. Since the swaps are interrelated in one way or another, we can make the indexes as nodes, and each swap between indexes an edge - if there is a clear path between the swaps, we can potentially work out a way to shift the values in the array respectively. With networkx, we can do this quite easily:

import itertools
import sys
import networkx as nx
import matplotlib.pyplot as plt

g = nx.Graph()

def pairwise(iterable):
    a, b = itertools.tee(iterable)
    next(b, None)
    return zip(a, b)

#patchy way to get individual color codes based on which function called swapall
ct = {'l': 'r', 'd': 'g', 'r': 'b', 'b': 'yellow', 'u': "purple", 'f': "black"}

def swapall(indexes):
    for i in indexes:
        g.add_node(i)
    for i, j in pairwise(indexes):
        g.add_edge(i, j, color=ct[sys._getframe().f_back.f_code.co_name])

def l():
    swapall([1, 17, 41, 40])
    swapall([4, 20, 44, 37])
    swapall([6, 22, 46, 35])
    swapall([9, 11, 16, 14])
    swapall([10, 13, 15, 12])

def d():
    swapall([14, 22, 30, 38])
    swapall([15, 23, 31, 39])
    swapall([16, 24, 32, 40])
    swapall([41, 43, 48, 46])
    swapall([42, 45, 47, 44])

def r():
    swapall([3, 38, 43, 19])
    swapall([5, 36, 45, 21])
    swapall([8, 33, 48, 24])
    swapall([25, 27, 32, 30])
    swapall([26, 29, 31, 28])

def b():
    swapall([1, 14, 48, 27])
    swapall([2, 12, 47, 29])
    swapall([3, 9, 46, 32])
    swapall([33, 35, 40, 38])
    swapall([34, 37, 39, 36])

def u():
    swapall([1, 3, 8, 6])
    swapall([2, 5, 7, 4])
    swapall([9, 33, 25, 17])
    swapall([10, 34, 26, 18])
    swapall([11, 35, 27, 19])

def f():
    swapall([6, 25, 43, 16])
    swapall([7, 28, 42, 13])
    swapall([8, 30, 41, 11])
    swapall([17, 19, 24, 22])
    swapall([18, 21, 23, 20])

jpt = {'l': l, 'd': d, 'r': r, 'b': b, 'u': u, 'f': f}

for c in 'ldrbuf':
    jpt[c]()

edges = g.edges()
colors = [g[u][v]['color'] for u,v in edges]
pos = nx.spring_layout(g, k=0.49, iterations=48)
nx.draw(g, edge_color=colors, with_labels=True, pos=pos)
plt.savefig('interaction.png')

After running, we can obtain the following graph:

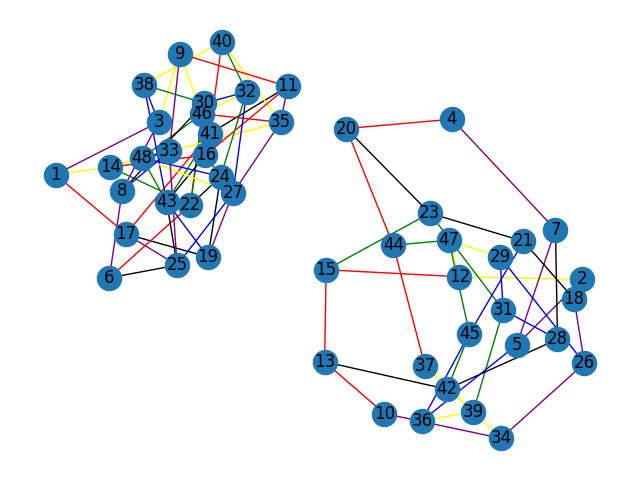
Yikes - that’s much more tangled than expected. However, there seems to be 2 distinct subgraphs that are not connected - what might that indicate?

Meanwhile, it has become blindingly clear that brute forcing is not the way to go:

Exception: java.lang.OutOfMemoryError thrown from the UncaughtExceptionHandler in thread "ForkJoinPool-1-worker-11"
Exception in thread "ForkJoinPool-1-worker-59" java.lang.OutOfMemoryError: Java heap space
Exception in thread "ForkJoinPool-1-worker-17" java.lang.OutOfMemoryError: Java heap space
Exception in thread "ForkJoinPool-1-worker-37" java.lang.OutOfMemoryError: Java heap space

Staring at the graph also gave me zero inspiration - it is as if the computation itself is magic, not the difficulty in reversing. Guess it’s time to pass the baton to my teammates…

Part 2: Logic and Rubik’s Cube

By alueft

I started looking through the challenge and rewriting some of the brute-force code in C++, although I wasn’t very optimistic about it running any faster. This was when I noticed multiple things:

• the above adjacency graph was split into two symmetric-looking subgraphs;
• there were six different colours; and
• my brain parsed the magic letters “ldrbuf” as “left down right back up front”, rather than something like “loader buffer”, because I don’t know anything about assembly.

Then, I grabbed the Rubik’s Cube (which happened to be within arm’s reach of me), and counted 9 tiles, times 6 faces, minus 6 centres that didn’t move: 9 * 6 - 6 = 48, which happened to be exactly the size of the array we were trying to sort. Once I read the problem description through a couple times, I noticed it carefully avoided using the word “cube”, and at this point I was convinced the challenge was solving a Rubik’s Cube.

Looking online for a solver, I found sagemath’s CubeGroup that maps the Rubik’s Cube’s face to numbers from 1-48, which is also exactly the values we see in the array. As the solved state for CubeGroup is also everything in order, just like what the program is testing, I plugged the scrambled array into sagemath:

sage: C = CubeGroup()
sage: C.solve(C.parse(magic))
"R2 F' R2 F2 L2 U2 R2 D2 F' U' L' B U D' R U B L2 D2 F2"

Converting that to what the program accepts is as simple as duplicating the character denoted by 2 twice, and ' thrice, which gives rrfffrrfflluurrddfffuuulllbudddrubllddff.

With that, we’re able to obtain the flag from the server:

$ nc magic3.sdc.tf 1337
== proof-of-work: disabled ==
Enter the magic passphrase for the flag: rrfffrrfflluurrddfffuuulllbudddrubllddff
sdctf{U2_m4st3rED_thE_DarK_MAg1c_0f_cub1ng}

Thoughts

Looking back, there are actually quite a bit of hints that we didn’t pick up - swapall swaps 4 indices since that’s the amount of faces affected in a single position in a single turn - and a total of 5 positions is changed (3 on the edge, 2 on the faces) on each turn, which maps to the 5 calls to swapall.

Therefore, the program was essentially initializing a cube, scrambling it, then asks us to give it the steps needed to solve it in any way. Naively brute forcing a solution for solving a Rubik’s cube ain’t exactly feasible with its mathematical complexity, so it all comes down to the revelation that what we are looking at is a Rubik’s cube scrambler.

This challenge is a prime example of how knowing the logic of a program doesn’t automatically grant you magical powers in solving what it intended you to solve - just like some of the other challenges that provide source code, maybe the ones where you can reverse easily are instead the hardest to solve.