Sabloom Text 6
Description
Finally, we have a text editor better than notepad.
⬇️ Download - Sabloom_Text_6_demo_win32.exe
Author - X3eRo0
Downloading and running the executable, I was greeted with the following window:
TL;DR
The Sabloom Text 6 app has a product registration form under Help>Register. When we enter X3eRo0 as the name and the flag as the serial, the product gets registered successfully.
Under the hood, the program checks if the serial (flag) is correct by XOR-ing it with some arbitrary values stored in memory, and then using the result as a set of instructions describing how to run through a 65 x 65 maze (which is hardcoded in memory). The program steps through the maze using the generated instructions, and it registers the product only if it successfully reaches the bottom right corner of the maze.
Exploring the Text Editor
To start, I played around with most of the text editor functions, but everything seemed pretty normal. However, I noticed at the top of the window was the title Sabloom Text 6 - [UNREGISTERED] which seemed a little odd… why would a simple CTF app need a product registration system?
Under Help>Register, I found a project registration form. I tried filling out the form with a random name and serial number, and I was presented with the message:
Please visit https://x3ero0.github.io/post/sabloom-license/ after the competition ends to Purchase License
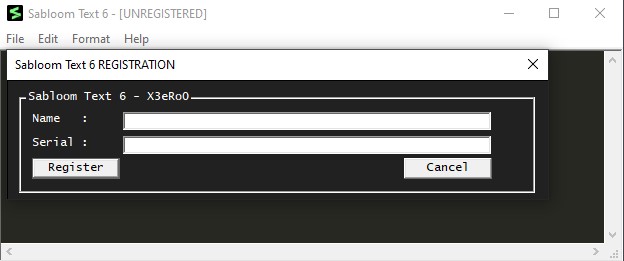
This seemed interesting. I developed an initial theory that I needed to enter the Name as X3ero0 and the Serial as the flag to register the product.
Analyzing the Binary
Getting Oriented
Using Ghidra, I was able to analyze the Sabloom_Text_6_demo_win32.exe binary and obtain the assembly and rough C code. The first thing I did was search for the string Please visit https://x3ero0.github.io/post/sabloom-license/ after the competition ends to Purchase License to try to find the code involved in checking a registration attempt. I found the code snippet below that seemed to display either a success message or an error message depending on the result of FUN_00402020:
// Read name and serial inputs
GetDlgItemTextA(param_1,0x3eb,(LPSTR)name_input,100);
GetDlgItemTextA(param_1,0x3ec,serial_input,100);
// Do something??? with name and serial
uVar1 = FUN_00402020(name_input,serial_input);
if ((char)uVar1 != '\0') { // Product gets registered
_DAT_004055b0 = 1;
MessageBoxA(param_1,"Product Registered","Sabloom Text 6 - Registered",0);
SetWindowTextA(h_00405384,"Sabloom Text 6 - X3eRo0");
EndDialog(param_1,0);
FUN_004022fb(local_c ^ (uint)&stack0xffffff0c,extraout_DL_01,in_stack_ffffff0c);
return;
}
// Product registration failed
_DAT_004055b0 = 0;
MessageBoxA(param_1,
"Please visit https://x3ero0.github.io/posts/sabloom-license/ after thecompetition ends to Purchase License"
,"Invalid Serial",0x10);
EndDialog(param_1,0);
FUN_004022fb(local_c ^ (uint)&stack0xffffff0c,extraout_DL_02,in_stack_ffffff0c);
return;
FUN_00402020 seemed promising. It looked like a decently complex algorithm that smelled like a reversing problem. It also seemed to only return true if the 1st and 5th characters of the name were X and o respectively which gave me more confidence in my theory that the registration name had to be X3ero0.
The function also only returned true if the serial’s 3rd and 5th parameters lined up with the name’s 2nd and 6th parameters. If my theory of the name being X3ero0 was correct, then the serial had to have the form XX3X0XXX... which matched up with the flag format of zh3r0{...}. This was enough to convince me that the Serial input needed to be the flag.
Here is the return statement of FUN_00402020 (modified for clarity, original code is the return statement of the unmodified Ghidra version here):
return maze_fail == 0 &&
reg_name_ptr[0] == 'X' &&
reg_name_ptr[1] == reg_serial_ptr[2] &&
reg_name_ptr[2] == reg_serial_ptr[9] &&
reg_name_ptr[3] == reg_serial_ptr[0xe] &&
reg_name_ptr[4] == 'o' &&
reg_name_ptr[5] == reg_serial_ptr[4];
Analyzing the Flag-Checking Functions
Convinced that FUN_00402020 (from here on let’s call it check_registration()) returning 1 was the answer, I examined what exactly was required for it return 1. I realized it called another function FUN_00401c50 and that this function had to return 0 for check_registration() to return 1.
I began heavily refactoring both functions. I made many changes (far too many to outline here), but both of the original Ghidra functions with comments but no refactoring can be found in the appendix below so you can cross-reference if you feel so inclined (the comments should match up): FUN_00402020 and FUN_00401c50.
I found that check_registration() first XOR-ed the serial with a chunk of memory. Then, it generated a 65 x 65 grid of bytes where each byte was either 0x00 or 0x01 from where it was stored in a more compressed format in memory. Finally, it put 0x33 at position (63, 63) in the grid and it passed both the XOR-ed serial and the byte grid to FUN_00401c50.
So what did FUN_00401c50 do with these two parameters? I definitely spent a while tracing through it, but I eventually realized that it was using the XOR-ed serial as instructions for moving through the 65 x 65 grid of bytes. However, moves through this grid could only be made if there was an unobstructed path of 0x01 bytes over which to travel. Additionally, this function only returned 0 if, after executing all the moves described by the XOR-ed serial, the byte we ended up on was 0x33 (recall this was position (63, 63)). All of this meant one thing: the 65 x 65 grid was a maze.
Here are the two refactored functions (from here one FUN_00401c50 will be called run_through_maze()):
uint check_registration(byte *reg_name_ptr, char *reg_serial_ptr)
{
if (strlen(reg_name_ptr) == 6) {
byte *moves_ptr = malloc(55);
byte *maze_ptr = malloc(4225);
if (moves_ptr != null && maze_ptr != null) {
memset(moves_ptr, 0, 55);
memset(maze_ptr, 0, 4225);
/*
* The moves to get through the maze are described by the
* result of xor-ing the serial number (the flag) with a
* set of values stored in memory.
*/
byte *xor_key_ptr = 0x403510;
int serial_len = strlen(reg_serial_ptr);
for (int i = 0; i < 54; i++) {
moves_ptr[i] = reg_serial_ptr[i % serial_len] ^ xor_key_ptr[i];
}
/*
* The maze 65 x 65 bytes where each byte is either 0x00
* or 0x01. However, the maze is stored in memory in a more
* compressed form as a 65 x 9 set of bytes. Each row of 9
* bytes represents a row of the maze, and each of the first
* 64 bits in this row represents one of the first 64 bytes
* in the expanded maze (the 9th byte is just padding). The
* 65th byte in the expanded maze is always 0x00, so we don't
* set it.
*/
char *compressed_maze_ptr = 0x403550;
byte* maze_cursor = maze_ptr;
char compressed_maze_byte;
for (int maze_row = 0; maze_row < (65 * 9); maze_row++) {
for (int j = 8; j > 0; j--) {
compressed_maze_byte = *compressed_maze_ptr;
for (int bitshift = 7; bitshift >= 0; bitshift++) {
*maze_cursor = (compressed_maze_byte >> bitshift) & 1;
maze_cursor++;
}
compressed_maze_ptr++;
}
compressed_maze_ptr++;
maze_cursor++;
}
// Put a '3' at the bottom right of the maze
maze_ptr[63 * 65 + 63] = '3';
/* Check that the moves calculated from the serial number
successfully get us through the maze */
int maze_fail = run_through_maze((int)maze_ptr, (int)moves_ptr);
free(moves_ptr);
free(maze_ptr);
/* Returns whether or not the serial number gave the correct
* directions through the maze. There are also some other
* weirldy specific checks to presumably give us a hint that
* the name should be X3eRo0 and that the flag is indeed the
* serial number.
*/
return maze_fail == 0 &&
reg_name_ptr[0] == 'X' &&
reg_name_ptr[1] == reg_serial_ptr[2] &&
reg_name_ptr[2] == reg_serial_ptr[9] &&
reg_name_ptr[3] == reg_serial_ptr[0xe] &&
reg_name_ptr[4] == 'o' &&
reg_name_ptr[5] == reg_serial_ptr[4];
}
}
return (uint)maze_ptr & 0xffffff00;
}
long run_through_maze(int maze_ptr, int moves_ptr)
{
void *expanded_moves_ptr = malloc(432);
memset(expanded_moves_ptr, 0, 432);
/* Expand each bit of the moves in move_ptr to be a whole byte
in expaned_moves_ptr */
byte *expanded_moves_cursor = expanded_moves_ptr;
for (int i = 0; i < 54; i++) {
moves_byte = *(byte *)(moves_ptr + i);
for (int bitshift = 7; bitshift >= 0; bitshift--) {
*expanded_moves_cursor = moves_byte >> (bitshift & 1);
expanded_moves_cursor++;
}
}
/*
* Starting at (1, 1) in the maze, we need to get to (63, 63)
* by only traveling over maze bytes that are 0x01. Whenever we
* move in a given direction, we take two steps. To change
* direction, we need to either increment or decrement (modulo 3)
* the move type by 1. The move types are as follows:
* 0 - Right
* 1 - Down
* 2 - Left
* 3 - Up
* Changes to the move types are described by either one or two
* bytes in extened_moves_ptr:
* 0 (single byte) - move type stays the same
* 11 (byte pair) - move type increments
* 10 (byte pair) - move type decrements
* Note: there is never a need to increment or decrement by 2
* (modulo 3) even though there are 4 move types because that
* would constitute going backwards
*/
int col = 1;
int row = 1;
int move_type = 0;
for (int move_num = 0; move_num < 432; move_num++) {
if (*(char *)((int)expanded_moves_ptr + move_num) == 1) {
move_num++;
if (*(char *)((int)expanded_moves_ptr + move_num + 1) == 1) {
move_type = (move_type + 1) % 3;
}
else {
move_type = (move_type - 1) % 3;
}
}
switch(move_type) {
case 0: // Right
if (maze_ptr[row * 65 + col + 1] == 1 &&
maze_ptr[row * 65 + col + 2] == 1) {
col = col + 2;
}
break;
case 1: // Down
if (maze_ptr[(row + 1) * 65 + col] == 1 &&
maze_ptr[(row + 2) * 65 + col] == 1) {
row = row + 2;
}
break;
case 2: // Left
if (maze_ptr[row * 65 + col - 1] == 1 &&
maze_ptr[row * 65 + col - 2] == 1) {
col = col - 2;
}
break;
case 3: // Up
if (maze_ptr[(row - 1) * 65 + col] == 1 &&
maze_ptr[(row - 2) * 65 + col] == 1) {
row = row - 2;
}
break;
}
}
free(expanded_moves_ptr);
if (maze_ptr[row * 65 + col] == '3') {
return 0;
}
return 0xffffffff;
}
Obtaining the Flag
Now that I knew that the problem involved using the flag XOR-ed with a chunk of memory as directions through a maze, the first step was to solve the maze.
I first generated the maze in python (I’d had enough C for one day). The mem_file simply contained copied and pasted hex codes at address 0x403550 from Ghidra:
def get_maze_from_mem():
mem_file = open(MEM_COMPRESSED_MAZE_PATH, 'r')
compressed_maze_hexs = mem_file.read().replace('\n', '').split(' ')
maze = []
for i in range(0, 585, 9):
compressed_maze_hexs_row = compressed_maze_hexs[i:i+9]
maze_row = []
for j in range(0, 8):
maze_bits = bin(int(compressed_maze_hexs_row[j], 16))[2:]
if len(maze_bits) < 8: maze_bits = '0' * (8 - len(maze_bits)) + maze_bits
for bit in maze_bits:
maze_row.append(int(bit))
maze_row.append(0)
maze.append(maze_row)
return maze
Here is the maze (-- is 0 and XX is 1 because it’s easier to see this way):

Next, I wrote an algorithm to solve the maze. The maze was small enought that could probably also be solved by hand, but I didn’t want to risk a typo:
def find_maze_moves(cur_pos, past_moves, maze, moves):
if cur_pos[0] == len(maze) - 2 and cur_pos[1] == len(maze[0]) - 2:
return True
if past_moves[-1] != 2 and maze[cur_pos[0]][cur_pos[1] + 1] == 1 and maze[cur_pos[0]][cur_pos[1] + 2] == 1:
if find_maze_moves([cur_pos[0], cur_pos[1] + 2], past_moves + [0], maze, moves):
moves.insert(0, 0)
return True
if past_moves[-1] != 3 and maze[cur_pos[0] + 1][cur_pos[1]] == 1 and maze[cur_pos[0] + 2][cur_pos[1]] == 1:
if find_maze_moves([cur_pos[0] + 2, cur_pos[1]], past_moves + [1], maze, moves):
moves.insert(0, 1)
return True
if past_moves[-1] != 0 and maze[cur_pos[0]][cur_pos[1] - 1] == 1 and maze[cur_pos[0]][cur_pos[1] - 2] == 1:
if find_maze_moves([cur_pos[0], cur_pos[1] - 2], past_moves + [2], maze, moves):
moves.insert(0, 2)
return True
if past_moves[-1] != 1 and maze[cur_pos[0] - 1][cur_pos[1]] == 1 and maze[cur_pos[0] - 2][cur_pos[1]] == 1:
if find_maze_moves([cur_pos[0] - 2, cur_pos[1]], past_moves + [3], maze, moves):
moves.insert(0, 3)
return True
return False
def solve_maze(maze):
moves = []
find_maze_moves([1, 1], [0], maze, moves)
return moves
The maze solving algorithm returned a list of numbers ranging from 1 to 4 because the run_through_maze() function from the binary analysis used the following map of numbers to moves:
- 1: right
- 2: down
- 3: left
- 4: up
Another useful piece of information to recall from the run_through_maze() function is that it used the following set of instr:
- 0: move type stays the same
- 11: move type is incremented modulo 3
- 10: move type is decremented modulo 3
Therefore, I could use the following function to determine the XOR-ed serial result from the moves through the maze:
def get_move_hexs(moves):
prev_move = 0
move_bits = ''
for move in moves:
if move - prev_move == 1 or (move == 0 and prev_move == 3):
move_bits += '11'
elif move - prev_move == -1 or (move == 3 and prev_move == 0):
move_bits += '10'
else:
move_bits += '0'
prev_move = move
return hex(int(move_bits, 2))[2:]
I was almost there. All I had to do was XOR the result of get_move_hexs(moves) with the chunk of memory at 0x403510 and I should have the flag. Again, the mem_file contained copied and pasted hex codes at address 0x403510 from Ghidra:
def decode_flag(move_hexs):
mem_file = open(MEM_XOR_KEY_PATH, 'r')
xor_hexs mem_file.read().replace(' ', '').replace('\n', '')
flag = ''
for i in range(0, len(move_hexs), 2):
xor_hex = hex(int(move_hexs[i:i+2], 16) ^ int(xor_hexs[i:i+2], 16))[2:]
flag += bytes.fromhex(xor_hex).decode('ascii')
flag_end = flag.find('}') + 1
return flag[:flag_end]
Victory! Here’s the flag: zh3r0{mAzes_w3Re_1nv3nteD_by_EgyptianS_cb3c82b9}
Appendix
FUN_00402020
uint __fastcall FUN_00402020(byte *param_1,char *param_2)
{
byte bVar1;
char cVar2;
byte bVar3;
byte bVar4;
byte bVar5;
byte bVar6;
byte bVar7;
byte bVar8;
byte bVar9;
byte bVar10;
byte bVar11;
void *_Dst;
byte *_Dst_00;
uint uVar12;
int iVar13;
uint extraout_EAX;
char *pcVar14;
byte *pbVar15;
byte *pbVar16;
byte *pbVar17;
char *local_20;
byte *local_14;
_Dst_00 = param_1;
pbVar16 = param_1;
do {
bVar1 = *pbVar16;
_Dst_00 = (byte *)((uint)_Dst_00 & 0xffffff00);
pbVar16 = pbVar16 + 1;
} while (bVar1 != 0);
if (pbVar16 + -(int)(param_1 + 1) == (byte *)0x6) {
_Dst = malloc(0x37);
_Dst_00 = (byte *)malloc(0x1081);
if ((_Dst != (void *)0x0) && (_Dst_00 != (byte *)0x0)) {
memset(_Dst,0,0x37);
memset(_Dst_00,0,0x1081);
pcVar14 = param_2;
do {
cVar2 = *pcVar14;
pcVar14 = pcVar14 + 1;
} while (cVar2 != '\0');
/*
* The moves to get through the maze are described by the
* result of xor-ing the serial number (the flag) with a
* set of values stored in memory.
*/
local_14 = &DAT_00403511;
pbVar16 = (byte *)((int)_Dst + 2);
pcVar14 = pcVar14 + -(int)(param_2 + 1);
do {
pbVar16[-2] = param_2[(uint)(pbVar16 + (-2 - (int)_Dst)) % (uint)pcVar14] ^ local_14[-1];
pbVar16[-1] = param_2[(uint)(pbVar16 + (-1 - (int)_Dst)) % (uint)pcVar14] ^ *local_14;
*pbVar16 = param_2[(uint)(local_14 + -0x40350f) % (uint)pcVar14] ^
pbVar16[(int)(&DAT_00403510 + -(int)_Dst)];
pbVar16[1] = param_2[(uint)(pbVar16 + (1 - (int)_Dst)) % (uint)pcVar14] ^
pbVar16[(int)(&DAT_00403511 + -(int)_Dst)];
pbVar16[2] = param_2[(uint)(pbVar16 + (2 - (int)_Dst)) % (uint)pcVar14] ^
pbVar16[(int)(&DAT_00403512 + -(int)_Dst)];
pbVar16[3] = param_2[(uint)(pbVar16 + (3 - (int)_Dst)) % (uint)pcVar14] ^
pbVar16[(int)(&DAT_00403513 + -(int)_Dst)];
pbVar16 = pbVar16 + 6;
local_14 = local_14 + 6;
} while ((int)(pbVar16 + (-2 - (int)_Dst)) < 0x36);
/*
* The maze 65 x 65 bytes where each byte is either 0x00
* or 0x01. However, the maze is stored in memory in a more
* compressed form as a 65 x 9 set of bytes. Each row of 9
* bytes represents a row of the maze, and each of the first
* 64 bits in this row represents one of the first 64 bytes
* in the expanded maze (the 9th byte is just padding). The
* 65th byte in the expanded maze is always 0x00, so we don't
* set it.
*/
local_20 = "";
pbVar16 = _Dst_00;
do {
local_14 = (byte *)0x8;
pbVar15 = pbVar16;
pcVar14 = local_20;
do {
cVar2 = *pcVar14;
uVar12 = 7;
pbVar17 = pbVar15;
do {
bVar1 = (byte)uVar12;
uVar12 = uVar12 - 1;
*pbVar17 = cVar2 >> (bVar1 & 0x1f) & 1;
pbVar17 = pbVar17 + 1;
} while (uVar12 < 0x80000000);
pcVar14 = pcVar14 + 1;
local_14 = (byte *)((int)local_14 + -1);
pbVar15 = pbVar15 + 8;
} while (local_14 != (byte *)0x0);
local_20 = local_20 + 9;
pbVar16 = pbVar16 + 0x41;
} while ((int)local_20 < 0x403799);
// Put a '3' at the bottom right of the maze
_Dst_00[0x103e] = 0x33;
/* Check that the moves calculated from the serial number
successfully get us through the maze */
iVar13 = FUN_00401c50((int)_Dst_00,(int)_Dst);
bVar11 = *param_1;
bVar1 = param_1[1];
bVar3 = param_1[2];
bVar4 = param_2[2];
bVar5 = param_2[9];
bVar6 = param_2[0xe];
bVar7 = param_1[4];
bVar8 = param_2[4];
bVar9 = param_1[3];
bVar10 = param_1[5];
free(_Dst);
free(_Dst_00);
/* Returns whether or not the serial number gave the correct
* directions through the maze. There are also some other
* weirldy specific checks to presumably give us a hint that
* the name should be X3eRo0 and that the flag is indeed the
* serial number.
*/
return extraout_EAX & 0xffffff00 |
(uint)(bVar10 == bVar8 &&
(bVar7 == 0x6f &&
(bVar9 == bVar6 &&
(bVar3 == bVar5 && (bVar1 == bVar4 && (bVar11 == 0x58 && iVar13 == 0))))));
}
}
return (uint)_Dst_00 & 0xffffff00;
}
FUN_00401c50
undefined4 __fastcall FUN_00401c50(int param_1,int param_2)
{
byte bVar1;
undefined8 uVar2;
undefined8 uVar3;
bool bVar4;
char cVar5;
void *_Dst;
int iVar6;
uint uVar7;
uint uVar8;
int iVar9;
uint uVar10;
int iVar11;
int in_FS_OFFSET;
int local_14;
int local_8;
_Dst = malloc(0x1b0);
local_8 = 1;
local_14 = 1;
memset(_Dst,0,0x1b0);
iVar11 = 0;
iVar9 = 0;
/* Expand each bit of the moves in move_ptr to be a whole byte
in expaned_moves_ptr */
do {
iVar6 = 0;
bVar1 = *(byte *)(iVar9 + param_2);
do {
cVar5 = (char)iVar6;
iVar6 = iVar6 + 1;
*(byte *)(iVar11 + (int)_Dst) = bVar1 >> (7U - cVar5 & 0x1f) & 1;
iVar11 = iVar11 + 1;
} while (iVar6 < 8);
iVar9 = iVar9 + 1;
} while (iVar9 < 0x36);
bVar4 = false;
uVar2 = rdtsc();
uVar7 = (uint)uVar2;
uVar3 = rdtsc();
uVar8 = (uint)uVar3;
uVar10 = 0;
if ((((uint)((ulonglong)uVar3 >> 0x20) | (int)uVar8 >> 0x1f) -
((uint)((ulonglong)uVar2 >> 0x20) | (int)uVar7 >> 0x1f) != (uint)(uVar8 < uVar7)) ||
(0x10000 < uVar8 - uVar7)) {
bVar4 = true;
}
/*
* Starting at (1, 1) in the maze, we need to get to (63, 63)
* by only traveling over maze bytes that are 0x01. Whenever we
* move in a given direction, we take two steps. To change
* direction, we need to either increment or decrement (modulo 3)
* the move type by 1. The move types are as follows:
* 0 - Right
* 1 - Down
* 2 - Left
* 3 - Up
* Changes to the move types are described by either one or two
* bytes in extened_moves_ptr:
* 0 (single byte) - move type stays the same
* 11 (byte pair) - move type increments
* 10 (byte pair) - move type decrements
* Note: there is never a need to increment or decrement by 2
* (modulo 3) even though there are 4 move types because that
* would constitute going backwards
*/
iVar11 = 0x41;
iVar9 = 0;
do {
iVar6 = iVar9 + 1;
if (*(char *)((int)_Dst + iVar9) == '\x01') {
iVar9 = iVar9 + 1;
if (*(char *)((int)_Dst + iVar6) == '\x01') {
uVar10 = uVar10 + 1 & 0x80000003;
if ((int)uVar10 < 0) {
uVar10 = (uVar10 - 1 | 0xfffffffc) + 1;
}
}
else {
uVar10 = uVar10 - 1 & 0x80000003;
if ((int)uVar10 < 0) {
uVar7 = uVar10 - 1 | 0xfffffffc;
uVar10 = uVar7 + 1;
if ((int)uVar10 < 0) {
uVar10 = uVar7 + 5;
}
}
}
}
iVar9 = iVar9 + 1;
switch(uVar10) {
case 0: // Right
if ((*(char *)(iVar11 + local_8 + 2 + param_1) != '\0') &&
(*(char *)(iVar11 + local_8 + 1 + param_1) != '\0')) {
local_8 = local_8 + 2;
}
break;
case 1: // Up
if ((*(char *)(param_1 + local_8 + 0x82 + iVar11) != '\0') &&
(*(char *)(iVar11 + local_8 + 0x41 + param_1) != '\0')) {
local_14 = local_14 + 2;
iVar11 = iVar11 + 0x82;
}
break;
case 2: // Left
if ((*(char *)(iVar11 + local_8 + -2 + param_1) != '\0') &&
(*(char *)(iVar11 + local_8 + -1 + param_1) != '\0')) {
local_8 = local_8 + -2;
}
break;
case 3: // Down
if ((*(char *)(local_8 + iVar11 + -0x82 + param_1) != '\0') &&
(*(char *)(iVar11 + local_8 + -0x41 + param_1) != '\0')) {
local_14 = local_14 + -2;
iVar11 = iVar11 + -0x82;
}
}
} while (iVar9 != 0x1b0);
free(_Dst);
if (((!bVar4) && ((*(uint *)(*(int *)(in_FS_OFFSET + 0x30) + 0x68) & 0x70) == 0)) &&
(*(char *)(local_14 * 0x41 + local_8 + param_1) == '3')) {
return 0;
}
return 0xffffffff;
}
